Question

In $\Delta MGN,MP \bot GN$. If $MG = a$ units, $MN = b$ units, $GP = c$ units and $PN = d$ units.
Prove that $\left( {a + b} \right)\left( {a - b} \right) = \left( {c + d} \right)\left( {c - d} \right)$.
               

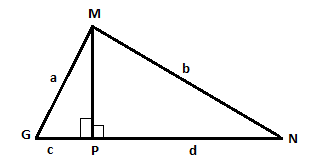
Answer 1

Hint: We need to know the concepts of Pythagoras theorem & formulas of algebraic expressions. Here we will have to apply Pythagoras theorem in the given triangle first and then equalize the perpendicular $MP$.

Complete step-by-step answer:
$\left( {a + b} \right)\left( {a - b} \right) = \left( {c + d} \right)\left( {c - d} \right)$
Using Pythagoras theorem ${a^2} = {b^2} + {c^2}$ in triangle $\Delta MGP$ and $\Delta MPN$we get –
$
  {a^2} = M{P^2} + {C^2} \\
  M{P^2} = {a^2} - {c^2}...........(i) \\
$
and,
$
  {b^2} = M{P^2} + {d^2} \\
  M{P^2} = {b^2} - {d^2}..........(ii) \\
$
$
  \therefore {a^2} - {c^2} = {b^2} - {d^2} \\
  {a^2} - {b^2} = {c^2} - {d^2} \\
$ [from equation $(i)$& $(ii)$]
By using formulae, ${a^2} - b{}^2 = \left( {a + b} \right)\left( {a - b} \right)$we get –
$\left( {a + b} \right)\left( {a - b} \right) = \left( {c + d} \right)\left( {c - d} \right)$
Hence, proved.

Note: In this type of question by generating two equations with the help of Pythagoras theorem is must. After that we can easily prove the given equation. While equating the linear equation formed by the given conditions, calculations & applying of formulas should be done carefully to avoid silly mistakes instead of knowing the concepts & formulations to be applied.