Question

In $ \Delta ABC,AX $ is the median. The internal bisectors of angles $ \angle AXB $ and $ \angle AXC $ meet AB and AC at L and M respectively. Prove that $ LM||BC $ .\[\]

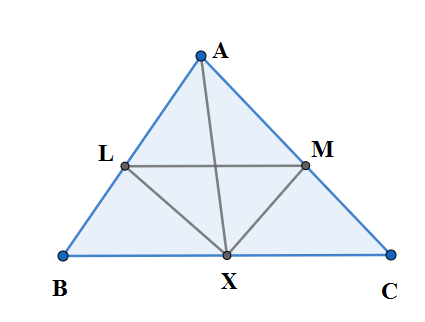
Answer 1

Hint: We use the angle bisector theorem in triangle ABX to prove $ \dfrac{XA}{XB}=\dfrac{AL}{LB} $ and we gain use angle bisector theorem in triangle ACX to prove $ \dfrac{XA}{XB}=\dfrac{AM}{MC} $ . We equate the right-hand sides to have $ \dfrac{AL}{LB}=\dfrac{AM}{LC} $ and use proportionality theorem in triangles to conclude $ LM||BC $ . \[\]

Complete step by step answer:
Let us observe the given diagram. \[\]

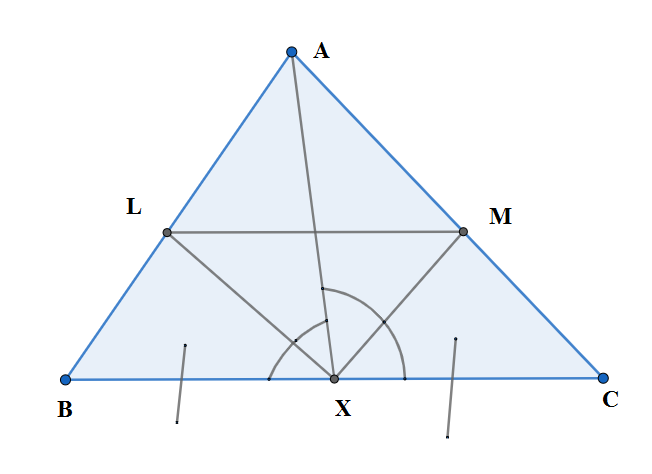
We are given that in $ \Delta ABC, AX $ is the median. $ XB=XC $ . It is also given that the internal bisectors of angles $ \angle AXB $ meet AB at L which means
\[\angle BXL=\angle AXL\]
We are given the internal bisector of $ \angle AXC $ meets AC at M which means
\[\angle AXM=\angle CXM\]

We know from the angle bisector theorem in a triangle that the angle bisector of an angle divides the length of the opposite side in a ratio equal to the length of corresponding adjacent sides. We observe the triangle AXB where XL is the angle bisector of $ \angle AXB $ whose opposite side is AB divided into LB and AL. The adjacent side $ \angle AXB $ and corresponding to LB and AL are XB and XA. So by angle bisector theorem we have;
\[\dfrac{XB}{XA}=\dfrac{LB}{AL}.........\left( 1 \right)\]
We observe the triangle AXC where XM is the angle bisector of $ \angle AXC $ whose opposite side is AC divided into LM and AM. The adjacent side $ \angle AXC $ and corresponding to MC and AM are XC and XA. So by angle bisector theorem we have;
\[\begin{align}
  & \Rightarrow \dfrac{XC}{XA}=\dfrac{MC}{AM} \\
 & \Rightarrow \dfrac{XB}{XA}=\dfrac{MC}{AM}\left( \because XB=XC \right)......\left( 2 \right) \\
\end{align}\]
We equate the right-hand sides of equations (1) and (2) since the left-hand sides are equal. We have;
\[\dfrac{LB}{AL}=\dfrac{MC}{AM}....\left( 3 \right)\]
We know from the proportionality theorem in a triangle that a line parallel to a side of a triangle intersects the other sides in two distinct points if and only if the line divides those sides in proportion. We see from (3) that the line LM divides the sides AB and AC in proportion. So LM will be parallel to the other side. Hence it is proved that
\[AM||BC\].

Note: We know that the median is the line segment that joins a vertex to the midpoint of the opposite side. Since the midpoint divides a line into two equal halves we got $ XB=XC $ which means the median divides the opposite side in ratio $ 1:1 $. We have used the converse of the proportionality theorem in the triangle here.