Question

In \[\Delta ABC,\angle ABC = {135^o}\] . Prove that \[A{C^2} = A{B^2} + B{C^2} + 4ar(\Delta ABC)\]

Answer 1

Hint: In this question a triangle \[ABC\] is given in which \[\angle ABC = {135^o}\] . This question can be solved when you construct a triangle \[ABC\] . With \[\angle ABC = {135^o}\] and extend the side \[BC\] for perpendicular to the vertex \[A\] . This is solved by using the basic formula of the area of the triangle.

Formula used: Here, we use the formula of area of triangle = \[\left( {\dfrac{1}{2} \times base \times height} \right)\] , algebraic identity that is \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\] and Pythagoras theorem as \[{H^2} = {P^2} + {B^2}\] .

Complete step-by-step solution:
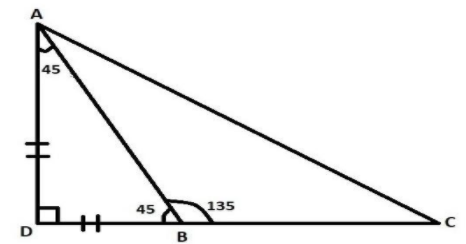
This question has a \[\Delta ABC\] where the area of the triangle is \[\left( {\dfrac{1}{2} \times base \times height} \right)\] used. Since, We know that the base angle is \[{135^\circ}\] , we can calculate its complement angle that will be \[180 - 135 = {45^\circ}\] according to the figure.
According to construction \[ADB\] is an isosceles triangle because \[\angle DAB = {45^\circ}\] , \[\angle DBA = {45^\circ}\] and \[AD\] is perpendicular on base \[BC\] .
\[\therefore AD = DB\] and \[BC + BD = DC\]
Now, the area of \[\Delta ABC = \dfrac{1}{2} \times AD \times BC\] by using the formula of an area of a triangle.
We can say that,

Using Pythagoras theorem:
\[A{C^2} = A{D^2} + D{C^2} \to (1)\]
Again using Pythagoras theorem:
\[A{B^2} = A{D^2} + B{D^2}\]
Simplifying the equation
\[ \Rightarrow A{D^2} = A{B^2} - B{D^2} \to (2)\]
Now putting the value of equation \[(2)\] in equation \[(1)\]
  Substituting the value of \[A{D^2}\]
\[ \Rightarrow A{C^2} = A{B^2} - B{D^2} + D{C^2}\]
As we know that \[BD = AD\]
We can rewrite the equation as \[A{C^2} = A{B^2} - A{D^2} + D{C^2} \to (3)\]
 As we know, \[BD = AD\]
\[D{C^2} = {(BC + AD)^2}\]
Simplifying using formula \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\]

Now we can calculate the area of \[\Delta ABC\] :
Multiplying both sides by 4
\[ \Rightarrow 4ar(\Delta ABC) = \left( {\dfrac{1}{2} \times AD \times BC} \right) \times 4\]
\[\therefore 4ar(\Delta ABC) = 2 \times AD \times BC \to (5)\]
Now, putting the value of equation \[(5)\] in equation \[(4)\] ; we have,
\[\therefore D{C^2} = {(BC)^2} + {(AD)^2} + 4ar(\Delta ABC) \to (6)\]
Now, putting the value of equation \[(6)\] in equation \[(3)\] ; we have,
\[\therefore A{C^2} = {(AB)^2} - {(AD)^2} + {(DC)^2}\]
After simplifying we get,
\[\therefore A{C^2} = A{B^2} + B{C^2} + 4ar(\Delta ABC)\] which is our required equation.
Hence Proved

Note: To solve these types of questions, we will use Pythagoras theorems to generate equations. Further we will also use properties of triangle and basic algebraic identities for simplification. Most of the time these questions can be easily solved by substituting values from one equation to another.