Question

In \[\Delta ABC,\angle A={{30}^{0}},\angle B={{40}^{0}},\angle C={{110}^{0}}\]. In\[\Delta PQR,\angle P={{30}^{0}},\angle Q={{40}^{0}},\angle R={{110}^{0}}\]. A student says that \[\Delta ABC\cong \Delta PQR\]by AAA congruence criterion. Is he justified? Why or Why not?

Answer 1

Hint: To solve the question, we have to construct PD and PE such that their lengths are equal to AB and AC, which is important to prove the given statement. To solve further, apply SAS symmetry, parallel lines properties and basic proportionality theorem to the formed triangles to ease the procedure of solving.

Complete step-by-step answer:

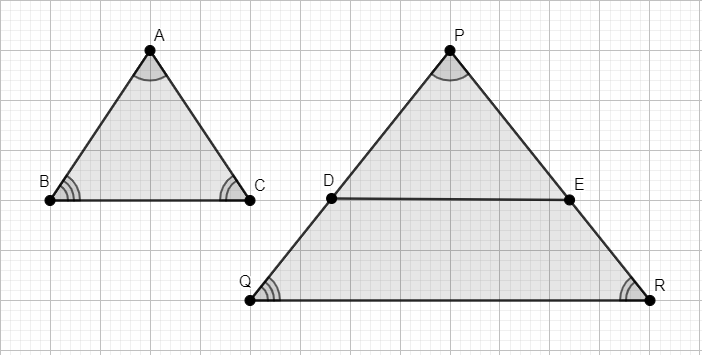
Let D, E be points on sides PQ and PR respectively.
Draw line segment DE in triangle PQR, such that PD = AB and PE = AC
Consider triangles \[\Delta PDE,\Delta ABC\]
PD = AB and PE = AC….. (1)
Since by construction
\[\angle P=\angle A={{30}^{0}}\]
Since it is given.
We know that SAS (Side- Angle- Side) symmetry that two triangles are congruent when two corresponding sides and one corresponding angle of the triangles are equal.
Thus, we get \[\Delta PDE,\Delta ABC\] are congruent triangles.
\[\Delta PDE\cong \Delta ABC\]
We know that in congruent triangle, all corresponding angles are equal.Thus, we get
\[\angle B=\angle D,\angle C=\angle E\]
\[\Rightarrow \angle Q=\angle D,\angle R=\angle E\]
Since it is given that \[\angle B=\angle Q={{40}^{0}},\angle C=\angle R={{110}^{0}}\]
We know that the corresponding angles are equalfor a pair of two parallel lines.
Thus, we can conclude that DE is parallel to QR.
We know that basic proportionality theorem states that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points thenthe other two sides are divided in the same ratio.
Thus, by applying the above theorem for triangle PQR, we get
\[\dfrac{DQ}{PD}=\dfrac{ER}{PE}\]
By adding 1 on both sides of equation, we get
\[\begin{align}
  & \dfrac{DQ}{PD}+1=\dfrac{ER}{PE}+1 \\
 & \dfrac{DQ+PD}{PD}=\dfrac{ER+PE}{PE} \\
\end{align}\]
We know that \[PD+DQ=PQ,PE+ER=PR\]. Thus, we get
\[\dfrac{PQ}{PD}=\dfrac{PR}{PE}\]
By substituting equation (1) in the above equation, we get
\[\dfrac{PQ}{AB}=\dfrac{PR}{AC}\]
Here the ratios are equal and we cannot say anything about the sides.
Therefore, in any two triangles having concurrent angles may have different sides. Thus, the two triangles may not be congruent. However, they may be identical in nature.

Note: The possibility of mistake can be, not constructing PD and PE such that their lengths are equal to AB and AC, which is important to prove the given statement. The other possible mistake can be, not applying SAS symmetry, parallel lines properties and basic proportionality theorem to the formed triangles, which will ease the procedure of solving.
Possible mistake is when they get equal ratios of the sides, students jump to the conclusion that sides are also equal, which is not true. In this way, they can go wrong.