Question

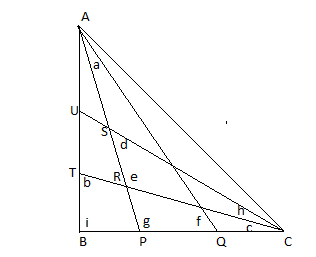
In $\Delta ABC$, what is the sum of angles $a + b + c + d + e + f + g + h + i$?

Answer 1

Hint: The sum of three angles of any triangle is $180{}^\circ $. This property is known as the Angle-Sum property of Triangle.

Complete step by step solution:
Angle-Sum property of a triangle makes the sum of three angles of a triangle to add up to $180{}^\circ $.
The labeling with letters – P, Q, R, S and T has been done to denote three different triangles in which Angle –Sum property of Triangle has to be applied.
In ΔAPQ, the three angles at vertices are: a, g and f.
Applying Angle-Sum property of triangle in ΔAPQ,
$a+g+f=180{}^\circ $ -- $(1)$
In ΔCRS, the three angles at vertices are: h, e and d.
Applying Angle-Sum property of triangle in ΔCRS,
$h+e+d=180{}^\circ $ -- $(2)$
In ΔBCT, the three angles at vertices are: i, c and b.
Applying Angle-Sum property of triangle in ΔBCT,
$i+c+b=180{}^\circ $ -- $(3)$
Summing equations: $(1)$, $(2)$, $(3)$ gives,
$a+g+f+h+e+d+i+c+b=180{}^\circ +180{}^\circ +180{}^\circ $
Rearranging the letters gives,
$a+b+c+d+e+f+g+h+i=540{}^\circ $
Therefore, indicates that the sum of angles a, b, c, d, e, f, g, h and i is equal to $540{}^\circ $.

Note:
As the sum of three angles of triangle is equal to $180{}^\circ $, the triangle can have at most one obtuse angle as value of obtuse angle is more than $90{}^\circ $ which means that two obtuse angles will make the sum of angles of triangle to be more than $180{}^\circ $.
The sum of $9$ angles comes to be $540{}^\circ $ because the sum of angles of three triangles were added up to arrive at the answer.