Question

In $\Delta ABC$, side CA $=$ side CB. On CB, a square BCED is constructed away from the triangle. If $\angle DAB=x$, then:
(a)$x$ depends upon the angles of the $\Delta ABC$
(b) $x$ is independent upon the angles of the $\Delta ABC$
(c) $x$ may be equal to $\angle CAB$
(d) $x$ is greater than ${{45}^{\circ }}$ but less than ${{90}^{\circ }}$

Answer 1

Hint: First of all, we are going to draw the figure according to the information given in the above problem. As side CA $=$ side CB so $\Delta ABC$ is an isosceles triangle. Also, we are going to use the property that in a triangle, an exterior angle is equal to the sum of the two interior opposite angles.

Complete step by step answer:
In the above problem, we have given a triangle ABC in which on the side CB, a square BCED is constructed away from triangle so we are drawing this information in the form of below figure-

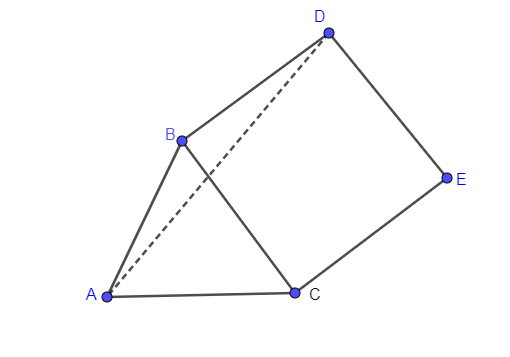
In the above problem, it is given that:
$CA=CB$
Now, we know that angles opposite to equal sides are equal so:
$\angle BAC=\angle ABC$
Now, in $\Delta ABC$, $\angle BCE$ is the exterior angle and we know that an exterior angle is equal to the sum of two interior opposite angles.
As BCED is a square so each angle is of ${{90}^{\circ }}$ then the value of $\angle BCE$ is also ${{90}^{\circ }}$. The opposite angles to the exterior angle BCE are:
$\angle BAC\And \angle ABC$
Now, an exterior angle $\angle BCE$ is equal to the sum of two interior opposite angles $\angle BAC\And \angle ABC$.
$\angle BCE=\angle BAC+\angle ABC$
We have shown above that $\angle BAC=\angle ABC$ so writing $\angle ABC=\angle BAC$ in the above we get,
$\begin{align}
  & {{90}^{\circ }}=\angle BAC+\angle BAC \\
 & \Rightarrow {{90}^{\circ }}=2\angle BAC \\
\end{align}$
Dividing 2 on both the sides we get,
$\begin{align}
  & \dfrac{{{90}^{\circ }}}{2}=\angle BAC \\
 & \Rightarrow {{45}^{\circ }}=\angle BAC \\
\end{align}$
It is given that $\angle DAB=x$ so if ACE will become a straight line then $\angle BAC$ may be equal to $\angle DAB$ or x may be equal to ${{45}^{\circ }}$.

Hence, the correct option is (c).

Note:
To solve the above problem, you must know the property of an exterior triangle that an exterior angle is equal to the sum of two interior opposite angles. And also that opposite angles of equal sides are equal. If you don’t have the knowledge of these properties then you are unable to solve this problem so make sure you are well aware of them.