Question

In $\Delta ABC$, side AB is produced to D so that $BD=BC$. If $\angle B={{60}^{{}^\circ }}$ and $\angle A={{70}^{{}^\circ }}$, prove that : $AD>AC$.

Answer 1

Hint: We will use some basic concepts of triangle to solve this problem, first we will use exterior angle property of triangle to show that $x=y={{30}^{{}^\circ }}$ and then we will use property that sum of all the three angles of triangles = ${{180}^{{}^\circ }}$ to find $\angle ACD$. In the last step we will compare $\angle A$ and $\angle C$ keeping in mind that the side opposite to the greater angle is longer.

Complete step-by-step answer:
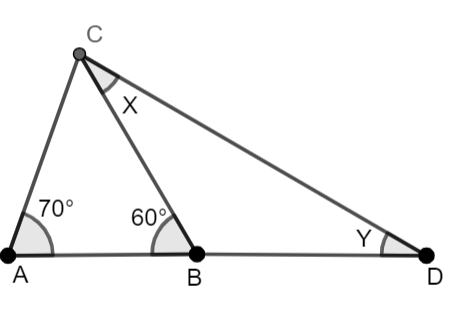
It is given in the question that ABC is a triangle in which side AB is produced to D. Side BD is equal to side BC and measure of $\angle A={{70}^{{}^\circ }}$and $\angle B={{60}^{{}^\circ }}$, then we have to prove that $AD>AC$. So, we can draw the diagram for this question as below.

We know that sum of all the three angles of a triangle is equal to ${{180}^{{}^\circ }}$, thus, in $\Delta ABC$ , we have,
$\angle A+\angle B+\angle C={{180}^{{}^\circ }}$, putting the values of angle A and angle B, we calculate angle C as follows
$70+60+\angle C=180$, solving further,
$130+\angle C=180$, thus,
$\angle C=180-130={{50}^{{}^\circ }}$.
Let us assume that $\angle BCD=x$ and $\angle BDC=y$. We know that an exterior angle of a triangle is an angle formed by one side of the triangle and the extension of an adjacent side of the triangles. Also, the measurement of an exterior angle of the triangle is equal to the sum of all the measures of the two non-adjacent interior angles.

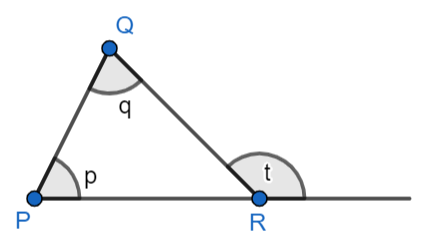
As in $\Delta PQR$, we have $\angle p+\angle q=\angle t$, angle t is an exterior angle.
Thus, in $\Delta BCD$, we have $\angle ABC=\angle BCD+\angle BDC$, therefore, we get $x+y={{60}^{{}^\circ }}$.
Also, in $\Delta ACD$, we have, $\angle A+\angle D+\angle C={{180}^{{}^\circ }}$. We know that $\angle A={{70}^{{}^\circ }}$, $\angle C={{\left( 50+x \right)}^{{}^\circ }}$ and \[\angle D={{y}^{{}^\circ }}\], thus, we get
${{70}^{{}^\circ }}+{{50}^{{}^\circ }}+{{x}^{{}^\circ }}+{{y}^{{}^\circ }}={{180}^{{}^\circ }}$.
But it is given that side BC is equal to side BD and angles opposite to equal sides of a triangle are equal, we get- $\angle x=\angle y$.
Using $\angle x=\angle y$ in equation $x+y={{60}^{{}^\circ }}$, we get
$\angle x+\angle x={{60}^{{}^\circ }}$, that is,
$2\angle x={{60}^{{}^\circ }}$, therefore
$\angle x=\dfrac{60}{2}={{30}^{{}^\circ }}$.
Therefore we get $\angle ACD=50+y=50+30={{80}^{{}^\circ }}$.
Now, we know that the side CD is opposite to angle A and side AD opposite to angle C, also $\angle C>\angle A$, also side opposite to greater angle is longer. From this we can say that $AD>AC$.
Hence proved.

Note: Students may stick initially if they do not know the exterior angle property of the triangle and the property that angle opposite to the equal sides are also equal. Many times students make mistakes in adding sum of angles thus it is recommended to learn all the properties of triangles before solving this type of question. Also, try to do calculations step by step in order to avoid mistakes.