Question

In $\Delta {\text{ABC}}$, right angled at ${\text{B}}$,${\text{AB}} = 24$, ${\text{BC}} = 7{\text{cm}}$. Determine:
(i) $\sin {\text{A, cos A}}$
(ii) $\sin {\text{C, cosC}}$

Answer 1

Hint: In this question first we will draw a right angle triangle whose sides are ${\text{AB}}$ and ${\text{BC}}$. Then, we will find the hypotenuse of the triangle by using Pythagoras theorem. After finding the hypotenuse we will use the formula of $\sin $ and $\cos $ to find out the answers.

Complete step-by-step solution:
(i) $\sin {\text{A, cos A}}$

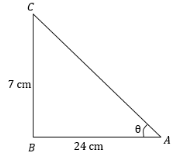
From the figure we can say that ${\text{AC}}$ is hypotenuse. ${\text{AB}} = 24\,cm$ and ${\text{BC}} = 7\,cm$ is given to us. We have to find ${\text{AC}}$
From the above figure, first we will find the hypotenuse of the right angle triangle. Therefore, from the figure we can write:
${\text{A}}{{\text{C}}^{\text{2}}}={\text{A}}{{\text{B}}^{\text{2}}}+{\text{B}}{{\text{C}}^{\text{2}}}$
Now, put the value of ${\text{AB}}$ and ${\text{BC}}$
$
   \Rightarrow {\left( {24} \right)^2} + {\left( 7 \right)^2} = 576 + 49 \\
   = 625
 $
We know that the $625$ is the square of $25$.
$ \Rightarrow {\text{AC}} = \sqrt {625} = 25$
Therefore, ${\text{AC = 25cm}}$ which is a hypotenuse of the right angle triangle.
Now, we know that \[\sin {\text{A}} = \dfrac{{{\text{BC}}}}{{{\text{AC}}}}\]. Therefore, we can write $\sin {\text{A}} = \dfrac{7}{{25}}$.
In the same way we know that $\cos {\text{A}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}}$. Therefore, we can write $\cos {\text{A}} = \dfrac{{24}}{{25}}$
Therefore, the answers are $\sin {\text{A}} = \dfrac{7}{{25}}$ and $\cos {\text{A}} = \dfrac{{24}}{{25}}$.
(ii) $\sin {\text{C, cosC}}$

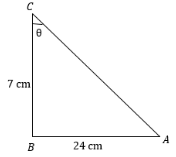
From the figure we can say that ${\text{AC}}$ is hypotenuse. ${\text{AB}} = 24$ and ${\text{BC}} = 7{\text{cm}}$ is given to us. We have to find ${\text{AC}}$
From the above figure, first we will find the hypotenuse of the right angle triangle. Therefore, from the figure we can write:
${\text{A}}{{\text{C}}^{\text{2}}}{\text{=A}}{{\text{B}}^{\text{2}}}{\text{+B}}{{\text{C}}^{\text{2}}}$
Now, put the value of ${\text{AB}}$ and ${\text{BC}}$
$
   \Rightarrow {\left( {24} \right)^2} + {\left( 7 \right)^2} = 576 + 49 \\
   = 625
 $
We know that the $625$ is the square of $25$.
$ \Rightarrow {\text{AC}} = \sqrt {625} = 25$
Therefore, ${\text{AC = 25cm}}$ which is a hypotenuse of the right angle triangle.
Now, we know that $\sin {\text{C}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}}$. Therefore, we can write $\sin {\text{C}} = \dfrac{{24}}{{25}}$
In the same way we know that \[\cos {\text{C}} = \dfrac{{{\text{BC}}}}{{{\text{AC}}}}\]. Therefore, we can write \[\cos {\text{C}} = \dfrac{7}{{25}}\].
Therefore, the answers are $\sin {\text{C}} = \dfrac{{24}}{{25}}$ and $\cos {\text{C}} = \dfrac{7}{{25}}$.

Note: The most important thing in the question is the diagram. So just try to draw a diagram first in this type of question. We also need to memorize the formula for $\sin $ and $\cos $. The other important thing is where we are taking that $\theta $ because it will help in finding $\sin $ and $\cos $. So be careful about these things.