Question

In \[\Delta \,\text{ABC}\], ray AD bisect \[\angle \text{A}\] and intersect BC in D. If \[\text{BC=a}\], \[\text{AC=b}\] and \[\text{AB=c}\], prove that
(i)\[\text{DC=}\dfrac{ab}{b+c}\] (ii) \[\text{BD=}\dfrac{ac}{b+c}\]

Answer 1

Hint: AD is the bisector of angle A and also triangle ADB and ACD are similar triangles. From this we get \[\dfrac{AB}{AC}=\dfrac{BD}{DC}\] and putting known values in this and using the information from the figure that BC is the summation of BD and DC we will solve the question.
Complete step-by-step solution -
The figure from the details mentioned in the question is:
 

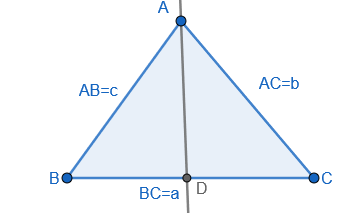
(i) In triangle ABC, since AD is the bisector of angle A and ADB and ACD are similar triangles, we see that
\[\,\Rightarrow \dfrac{AB}{AC}=\dfrac{BD}{DC}.......(1)\]
We know that \[\text{AB=c}\], \[\text{AC=b}\] and \[\text{BC=a}\].
So now substituting the values of AB, AC in equation (1) we get,
 \[\,\Rightarrow \dfrac{c}{b}=\dfrac{BD}{DC}.......(2)\]
Now adding 1 to both sides of the equation (2) we get,
 \[\begin{align}
  & \,\Rightarrow \dfrac{c}{b}+1=\dfrac{BD}{DC}+1 \\
 & \,\Rightarrow \dfrac{c+b}{b}=\dfrac{BD+DC}{DC}.......(3) \\
\end{align}\]
Now we know from the figure that the summation of BD and DC is BC and length of BC is a. Using this information in equation (3) we get,
 \[\begin{align}
  & \,\Rightarrow \dfrac{c+b}{b}=\dfrac{BC}{DC} \\
 & \,\Rightarrow \dfrac{c+b}{b}=\dfrac{a}{DC}........(4) \\
\end{align}\]
Now solving for DC in equation (4) by cross multiplying we get,
 \[\,\Rightarrow DC=\dfrac{ab}{b+c}......(5)\].
Hence proved.
(ii) Now from the figure we know that BC is the summation of BD and DC. So here we need to find BD.
So BD is BC minus DC and also we know that BC is equal to a. Using this information, we get,
 \[\,\Rightarrow \text{BC=a}\]
Now from figure we get,
 \[\,\Rightarrow \text{BD+DC=a}........\text{(6)}\]
Substituting the value of DC from equation (5) in equation (6) we get,
 \[\,\Rightarrow \text{BD+}\dfrac{ab}{b+c}\text{=a}........\text{(7)}\]
Rearranging and simplifying equation (7) by isolating BD and cancelling similar terms and solving for it we get,
 \[\begin{align}
  & \,\Rightarrow \text{BD=}a-\dfrac{ab}{b+c} \\
 & \,\Rightarrow BD=\dfrac{a(b+c)-ab}{b+c} \\
 & \,\Rightarrow BD=\dfrac{ab+ac-ab}{b+c} \\
 & \,\Rightarrow BD=\dfrac{ac}{b+c} \\
\end{align}\]
Hence proved.

Note: These types of questions initially seem tough but once we draw the figure from the details given in the question everything becomes clear. We may get confused in solving equation (2) but when we add 1 to both sides we get BC in the right hand side of the equation and then there is only one unknown DC.