Question

In \[\Delta ABC\], in which \[\angle C={{90}^{\circ }},\angle ABC=\theta \], \[BC=21\]units, \[AB=29\]units.

Show that \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\dfrac{41}{841}\]

Answer 1

Hint: In this question, we first need to draw the diagram to get the values of sine and cosine by using the trigonometric ratios. Then substitute the respective values of the sine and cosine in the left hand side of the given expression to get the result.

\[\sin \theta =\dfrac{AC}{AB}\]

\[\cos \theta =\dfrac{BC}{AB}\]

Complete step-by-step answer:


Now, from the given values in the question we have

\[BC=21,AB=29\]

Now, let us draw the diagram with the given conditions

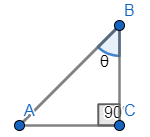
As the triangle is a right angled triangle we have

\[A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}\]

Now, on substituting the respective values we get,

\[\Rightarrow {{29}^{2}}=A{{C}^{2}}+{{21}^{2}}\]

Now, on rearranging the terms we get,

\[\Rightarrow A{{C}^{2}}={{29}^{2}}-{{21}^{2}}\]

Now, this can be also written as

\[\Rightarrow A{{C}^{2}}=841-441\]

Now, on further simplification we get,

\[\Rightarrow A{{C}^{2}}=400\]

Let us now apply square root on both sides

\[\therefore AC=20\]

Now, from the trigonometric ratios we have

\[\Rightarrow \sin \theta =\dfrac{AC}{AB}\]

Now, on substituting the respective values we get,

\[\Rightarrow \sin \theta =\dfrac{20}{29}\]

Now, from the trigonometric ratios we also have

\[\Rightarrow \cos \theta =\dfrac{BC}{AB}\]

Now, on substituting the respective values we get,

\[\Rightarrow \cos \theta =\dfrac{21}{29}\]

Let us now consider the given expression in the question

\[\Rightarrow {{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\dfrac{41}{841}\]

Now, on considering the left hand side we get,

\[\Rightarrow {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \]

Now, on substituting the respective values in the above expression we get,

\[\Rightarrow {{\left( \dfrac{21}{29} \right)}^{2}}-{{\left( \dfrac{20}{29} \right)}^{2}}\]

Now, this can be further written as

\[\Rightarrow \dfrac{441}{841}-\dfrac{400}{841}\]

Now, on further simplification we get,

\[\Rightarrow \dfrac{41}{841}\]

Hence, \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\dfrac{41}{841}\]


Note:

Instead of finding the value of the side AC to find the sine function value we can directly find the cosine function value from the given conditions and then use trigonometric identity to get the value of sine. Both the methods give the same result.
It is important to note that while finding the values of sine and cosine we need to substitute the respective values because interchanging the values of numerator and denominator or neglecting any of the terms changes the result completely.