Question

In $\Delta ABC$, if $\angle A = {90^ \circ }$ and $AD \bot BC$, then the correct statement is
1) $A{D^2} = \left( {BD} \right)\left( {DC} \right)$
2) $A{B^2} = BC \times BD$
3) $A{C^2} = BC \times DC$

Answer 1

Hint: After drawing a perpendicular from $A$, we get two triangles, we will first prove $\angle CAD = \angle B$ using properties of triangle. Then, we will find the value of $\tan B$ and $\tan \angle CAD$ from the triangles and then will equate these values to get the desired result.

Complete step-by-step answer:
First of all, let us draw the figure of the given statement. $\vartriangle ADB$ and $CDA$.

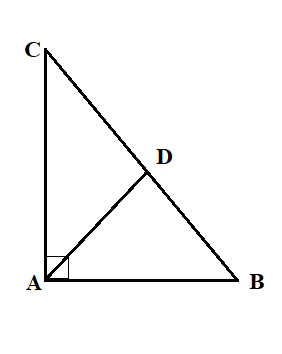
Here, $\angle A = {90^ \circ }$ and $AD \bot BC$.
In $\vartriangle ABC$, $\angle A + \angle B + \angle C = {180^ \circ }$ using angle sum property.
Then,
$
  {90^ \circ } + \angle B + \angle C = {180^ \circ } \\
   \Rightarrow \angle B = {90^ \circ } - \angle C \\
$
In $\vartriangle CAD$,
 $
  \angle ADC + \angle CAD + \angle ACD = {180^ \circ } \\
   \Rightarrow {90^ \circ } + \angle CAD + \angle ACD = {180^ \circ } \\
   \Rightarrow \angle CAD + \angle C = {90^ \circ } \\
   \Rightarrow \angle CAD = {90^ \circ } - \angle C \\
$
Hence, $\angle CAD = \angle B$
We will find the required result using trigonometry.
As we know that $\tan \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Base}}}}$
Now, in $\vartriangle ADB$, we will find the value of $\tan B$ using trigonometry.
$\tan B = \dfrac{{AD}}{{BD}}$ eqn. (1)
Also, we can find the value of $\tan B$, from $CDA$
$\tan \angle CAD = \dfrac{{CD}}{{AD}}$
$\tan B = \dfrac{{CD}}{{AD}}$ eqn. (2)
From equation (1) and (2), we will get,

$\dfrac{{AD}}{{BD}} = \dfrac{{CD}}{{AD}}$
On cross-multiplying the above equation, we will get,
$
  AD \times AD = CD \times BD \\
   \Rightarrow A{D^2} = BD \times CD \\
$
Hence, option A is correct.
Note: Students must know the trigonometric ratios, like $\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$, $\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$ and $\tan \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Base}}}}$. We can also do this question by applying Pythagoras theorem in the right triangles, $\vartriangle ADC$ and $\vartriangle ADB$.