Question

In $ \Delta ABC $ , if $ a=5 $ , $ b=4 $ and $ A=\dfrac{\pi }{2}+B $ then $ \tan C= $ ?
(a) $ \dfrac{9}{40} $
(b) 4
(c) 2.5
(d) 1.45

Answer 1

Hint: We will use the fact that sum of all angles of a triangle is $ 180{}^\circ $ to find the angle $ C $ in terms of angle $ B $ . Then we will use the relations between trigonometric ratios of angle $ \dfrac{\pi }{2}-x $ to compute the value of $ \tan C $ . We will also use the double angle formula for the tangent function, which is given as $ \tan 2x=\dfrac{2\tan x}{1-{{\tan }^{2}}x} $ . We will also use the law of sines to obtain the value of $ \tan B $ .

Complete step by step answer:
The rough diagram of such a triangle would look like the following,

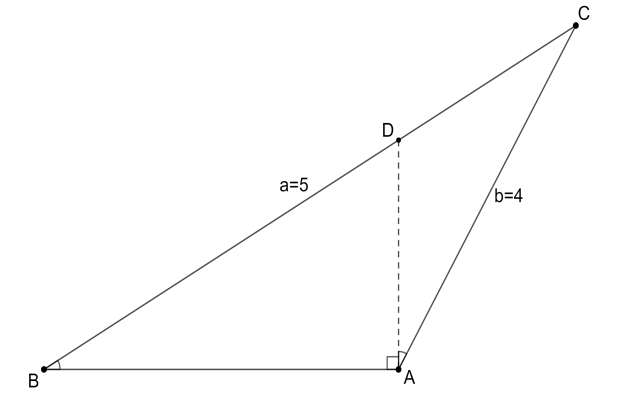
We know that the sum of all angles of a triangle is $ 180{}^\circ $ . Therefore, we have
 $ A+B+C=\pi $
Substituting $ A=\dfrac{\pi }{2}+B $ in the above equation we get,
 $ \begin{align}
  & \dfrac{\pi }{2}+B+B+C=\pi \\
 & \therefore C=\dfrac{\pi }{2}-2B \\
\end{align} $
Now, we have to find the value of $ \tan C $ . Using the value of angle $ C $ , we get
 $ \tan C=\tan \left( \dfrac{\pi }{2}-2B \right) $
We have relations between trigonometric ratios of angle $ \dfrac{\pi }{2}-x $ . According to these relations, we know that $ \tan \left( \dfrac{\pi }{2}-\theta \right)=\cot \theta $ . We also know that $ \cot \theta =\dfrac{1}{\tan \theta } $ . Combining these two facts, we have $ \tan \left( \dfrac{\pi }{2}-\theta \right)=\dfrac{1}{\tan \theta } $ . So, we can write the value of $ \tan C $ as the following,
 $ \tan C=\dfrac{1}{\tan 2B}....(i) $
For any triangle $ \Delta ABC $ , we have the law of sines, which is given as
 $ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} $
where $ a,b,c $ are the lengths of sides opposite to the angles $ A,B,C $ respectively.
For the given triangle, we have $ a=5 $ , $ b=4 $ . So, using the law of sines, we get
 $ \begin{align}
  & \dfrac{5}{\sin A}=\dfrac{4}{\sin B} \\
 & \therefore 5\sin B=4\sin A \\
\end{align} $
Substituting the value $ A=\dfrac{\pi }{2}+B $ in the above equation, we have
 $ 5\sin B=4\sin \left( \dfrac{\pi }{2}+B \right) $
We know that $ \sin \left( \dfrac{\pi }{2}+\theta \right)=\cos \theta $ . Therefore, we have
 $ \begin{align}
  & 5\sin B=4\cos B \\
 & \Rightarrow \dfrac{\sin B}{\cos B}=\dfrac{4}{5} \\
 & \therefore \tan B=\dfrac{4}{5} \\
\end{align} $
Now, we will use the double angle formula for the tangent function to find the value of $ \tan 2B $ . The double angle formula is given by $ \tan 2x=\dfrac{2\tan x}{1-{{\tan }^{2}}x} $ . So, we have the following,
 $ \tan 2B=\dfrac{2\tan B}{1-{{\tan }^{2}}B} $
Substituting $ \tan B=\dfrac{4}{5} $ in the above formula, we get
 $ \begin{align}
  & \tan 2B=\dfrac{2\times \dfrac{4}{5}}{1-{{\left( \dfrac{4}{5} \right)}^{2}}} \\
 & \Rightarrow \tan 2B=\dfrac{\dfrac{8}{5}}{1-\dfrac{16}{25}} \\
 & \Rightarrow \tan 2B=\dfrac{\left( \dfrac{8}{5} \right)}{\left( \dfrac{9}{25} \right)} \\
 & \Rightarrow \tan 2B=\dfrac{8}{5}\times \dfrac{25}{9} \\
 & \therefore \tan 2B=\dfrac{40}{9} \\
\end{align} $
Substituting this value in equation $ (i) $ , we have
 $ \begin{align}
  & \tan C=\dfrac{1}{\left( \dfrac{40}{9} \right)} \\
 & \therefore \tan C=\dfrac{9}{40} \\
\end{align} $
Hence, the correct option is (a).

Note:
 It is important to know the law of sines to solve this question. We should be familiar with the trigonometric functions and their relations amongst themselves for adding or subtracting angles like $ \dfrac{\pi }{2},\pi $, etc. The double angle formulae and the half-angle formulae are useful in calculations in such type of questions. We should do the calculations explicitly to avoid making any errors in the calculations.