Question

In $\Delta ABC,{\text{ }}DE||BC$and $AC = 5.6$cm, $AE = 2.1$cm, then find $AD:DB$ .

Answer 1

Hint:First try to show that the triangle $\Delta DAE$ and $\Delta BAC$ are similar using AAA similarity rule and then use the property of similarity that the ratio of the corresponding sides are same, to get the relation between the sides AB and AD, then use these sides to get the desired result.

Complete step-by-step answer:
We have given that, in $\Delta ABC,{\text{ }}DE||BC$ and $AC = 5.6$cm, $AE = 2.1$cm.
The goal is to find the ratio $AD:DB$.
First create a figure of $\Delta ABC$, which defines the given data:

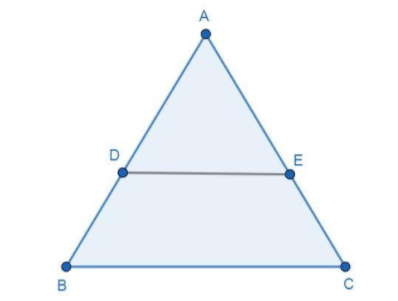
Take two triangles, $\Delta DAE$ and $\Delta BAC$, we can see that
$\angle A = \angle A$ (Common angle in both triangles)
$\angle ADE = \angle ABC$(Angle formed by transversal line)
$\angle AED = \angle ACB$(Angle formed by transversal line)
Then, using the AAA rule of similarity, we can say that $\Delta DAE$ is similar to $\Delta BAC$. That is
$\Delta DAE \sim \Delta BAC$
Then using the property of similarity, that the ratio of the corresponding sides is same, so we have
$\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}$
Substitute the values $AC = 5.6$cm and $AE = 2.1$cm into the above equation, then we have
$\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{2.1}}{{5.6}}$
Simplify the values:
$\dfrac{{AD}}{{AB}} = \dfrac{3}{8}$
$ \Rightarrow AB = \dfrac{8}{3}AD$
Now, we can take the value of $DB$ as the difference AB and AD:
$DB = AB - AD$
Substitute the value of $AB$ in the equation, then we have
$ \Rightarrow DB = \dfrac{8}{3}AD - AD$
Simplify the difference:
$ \Rightarrow DB = AD\left( {\dfrac{8}{3} - 1} \right)$
$ \Rightarrow DB = AD\left( {\dfrac{5}{3}} \right)$
$ \Rightarrow \dfrac{{AD}}{{DB}} = \dfrac{3}{5}$
So, the required ration has the value given as:
$AD:DB = 3:5$

Note:There are three ways to show that the given triangles are similar:
First is AA rule in which, if we show that any two angles of both the triangles are same, then we can say that the triangles are similar.
Second is the SAS rule in which we have to show that two sides of both the triangles are same and also the angle corresponding to the third side is also same, then we say that the triangles are similar.
Finally, the third rule is SSS in which, if we show that all the three sides of both the triangles are same then we can say that the triangles are similar.