Question

In $\Delta ABC,$ $DE$ is parallel to $BC, AD=x, BD=x+1, AE=x+3$ and $EC=x+5.$ Find $x.$

Answer 1

Hint: We will use the Basic Proportionality theorem to find the value of $x.$ The theorem states that if a line is drawn parallel to one side of a triangle intersecting the other two sides of a triangle in distinct points, then the other two sides are divided in the same ratio.

Complete step by step solution:
Let us consider the given triangle $\Delta ABC.$
In this triangle, the line $DE$ is parallel to $BC.$ Also, from the given information, we can conclude that the line intersects the other two sides of the triangle in distinct points.
It is given that $AD=x, BD=x+1, AE=x+3$ and $CE=x+5.$
Given below is the triangle satisfying the given information.

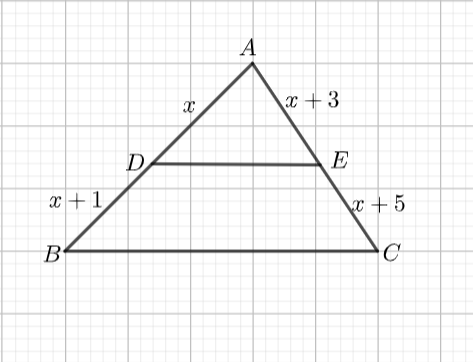
We are asked to find the value of $x.$
Now, we will use the Basic Proportionality theorem.
By the theorem, if a line is drawn parallel to one side of a triangle intersecting the other two sides of the triangle, then the other two sides are divided in the same ratio.
In this case also, as we can see, the line $DE$ is drawn in a way that it is parallel to the side $BC$ of the triangle and that it is intersecting the other two sides of the triangle.
We can conclude that the sides of the triangle are divided in the same ratio.
So, we will get $\dfrac{AD}{BD}=\dfrac{AE}{CE}.$
Now, we will get $\dfrac{x}{x+1}=\dfrac{x+3}{x+5}.$
After we transpose the terms, we will get $x\left( x+5 \right)=\left( x+1 \right)\left( x+3 \right).$
So, we will get ${{x}^{2}}+5x={{x}^{2}}+4x+3.$
From this, we will get $5x-4x=x=3.$
Hence $x=3.$

Note: The converse of the Basic Proportionality is also true. The converse theorem of Proportionality states that if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side of the triangle.