Question

In $\Delta ABC$ , D and E are the midpoints of AB and AC respectively, then the area of $\Delta ADE$ is
A. $4 \times $ Area of $\Delta ABC$
B. $\dfrac{1}{4} \times $Area of $\Delta ABC$
C. $2 \times $ Area of $\Delta ABC$
D. $\dfrac{1}{2} \times $Area of $\Delta ABC$

Answer 1

Hint:

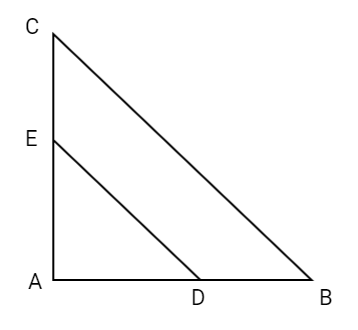
Start by drawing the diagram of the supposed figure showing the triangles and their midpoints D and E on AB and AC respectively. Form a relation between AB and AD , similarly, AE and AC. Use the formula for the area of the triangle and the relation formed in order to find the required relation of areas.

Complete step-by-step answer:
Given, D and E are the midpoints of AB and AC respectively.
Let us draw a triangle ABC with D and E as midpoints of AB and AC respectively.
Since D is the midpoint of AB , it means AB will be twice the AD.
$\therefore 2AD{\text{ }} = {\text{ }}AB \to eqn.1$
Similarly, E is the midpoint of AC , it means AC will be twice of AE.
$\therefore 2AE{\text{ }} = {\text{ }}AC \to eqn.2$
Now , we know Area of triangle = $\dfrac{1}{2} \times base \times height$
So, Area of$\Delta ABC$ = $\dfrac{1}{2} \times AC \times AB$
Since, ADE also from a triangle
$\dfrac{1}{2} \times AE \times AD$
From eqn. 1 and eqn. 2 , we get
$
   = \dfrac{1}{2} \times \dfrac{{AC}}{2} \times \dfrac{{AB}}{2} \\
   = \dfrac{1}{2} \times \dfrac{1}{2} \times AC \times AB \\
$
$ = \dfrac{1}{4}$(area of$\Delta ABC$)
Therefore , Area of$\Delta ADE$ $ = \dfrac{1}{4}$(Area of$\Delta ABC$)

So, the correct answer is “Option B”.

Note: Such similar questions based upon area can be asked with different geometrical shapes such as rectangle , parallelogram , sector of a circle, etc. In such problems use the data given in the question and apply the properties of the figure or shape given.