Question

In $\Delta ABC$, $\angle B={{30}^{0}},\angle C={{80}^{0}}\And \angle A={{70}^{0}}$then:
A) AB > BC < AC
B) AB < BC > AC
C) AB > BC > AC
D) AB < BC < AC

Answer 1

Hint: There is a theorem that the side opposite to a larger angle is longer so we are going to use this theorem in the above question and then according to the order of the angle we will decide the order of the sides of the triangle.

Complete step-by-step answer:
In the below figure, we have shown a $\Delta ABC$ having different values of angles A, B and C.

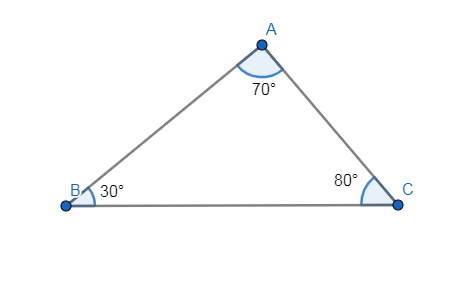
We have to find the order of the sides of the $\Delta ABC$ so we are going to use the theorem which states that the side which is opposite to the larger angle is longer.
From the above figure, we can see that angle C is the largest among angles A, B and C so by the theorem that we have just described the side opposite to angle C i.e. AB is the longest among all the sides of the $\Delta ABC$.
Now, the smallest angle in the above figure is angle B so the side opposite to angle B is AC which is the smallest side among all the three sides of $\Delta ABC$.
And the angle A is the second largest angle among all the angles of $\Delta ABC$ so the side opposite to angle A is BC which would be the second largest side after AB among all the three sides of $\Delta ABC$.
So, the order of the sides from the above discussion is AB > BC > AC.
Hence, the correct option is (C).

Note: In the theorem which states that the side opposite to a larger angle is the longer side among all the sides of a triangle. The vice versa of this theorem is also true that the angle opposite to a larger side is the longest among all the sides of a triangle. You might get a problem in which unequal sides are given and you have to find the order of the angles so you can apply this theorem that we have just discussed.