Question

In $\Delta $ABC, AE is the external bisector of $\angle $A , meeting BC produced at E . If AB = 10cm , AC = 6cm and BC=12cm , then find CE .

Answer 1

Hint: In order to solve the given question , we will be using the theorem which states that The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle . Also to perform some calculations to simplify the given equation by somewhere using equivalent equations and algebraic identities . Equivalent equations are said to be algebraic equations that may have the same solutions if we add or subtract the same number to both sides of an equation - Left hand side or Right hand side of the equal sign . Or we can multiply or divide the same number to both sides of an equation - Left hand side or Right hand side of the equal to sign with the method of simplification .

Complete step by step solution:
We are given AE is the external bisector of $\angle $A , meeting BC produced at E . If AB = 10cm , AC = 6cm and BC=12cm .
Now let's consider CE = $x$ cm

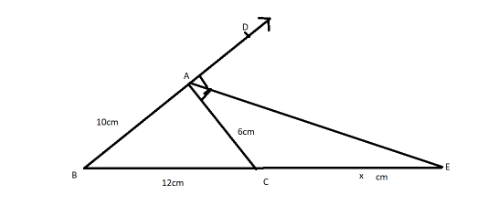
BE = \[\left( {12 + x} \right)\]cm
Since AE is the bisector of the exterior angle $\angle $A .
So , $\dfrac{{BE}}{{CE}} = \dfrac{{AB}}{{AC}}$ as , The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle .
Now we will substitute the values in the ratios as given ,
$\dfrac{{12 + x}}{x} = \dfrac{{10}}{6}$
Now multiply both sides by 6 and x, we get –
$6(12 + x) = 10x$
Open the bracket and perform multiplication with each term ,
$72 + 6x = 10x$
Perform calculation with like terms , we get =
$
  10x - 6x = 72 \\
  4x = 72 \\
  x = \dfrac{{72}}{4} \\
  x = 18 \;
 $
Therefore , the value of CE is 18cm.
So, the correct answer is “ CE is 18 cm”.

Note: In equivalent equations which have identical solutions we can perform multiplication or division by the same non-zero number both L.H.S. and R.H.S. of an equation .
In an equivalent equation which has an identical solution we can raise the same odd power to both L.H.S. and R.H.S. of an equation .
Remember the properties and apply appropriately .
Try to solve the question using the diagram which makes it visual and easy to understand .
Cross check the answer and always keep the final answer simplified .