Question

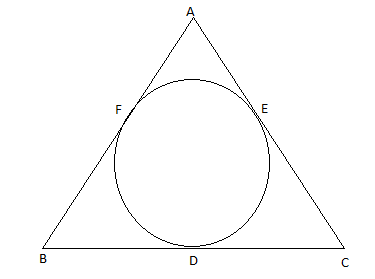
In $\Delta ABC$, a circle is inscribed .If $AB = 13cm,BC = 14cm$ and $AE = 7{\text{cm}}$. Find $AC$.

Answer 1

Hint: We will use the fact that: tangents from the same external points are equal in length. Using the fact, we will have some equations for the sides for the triangle then using those equations and length mentioned in the questions, we will have our answer.

Complete step-by-step answer:
We see that $AB$ and $AC$ touch the circle at circle $F$ and $E$ respectively and nowhere else.
Hence we can say that $AB$ and $AC$ the tangents to the circle.
Because the tangent is a straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point.
Now we will use the fact that: Tangents from the same external points are in equal length.
Now tangents $AB$ and $AC$ cut at $F$ and $E$ respectively coming from the same point $A$
We are already given in the question that $AE = 7cm$
∴$AF = AE = 7cm$ (Since Tangents of the circle)
We are already given in the question that $AB = 13{\text{cm}}$
We can see in the figure clearly that\[AB = BF + AF\]
Now we have to find out $BF$ we can write it as,
$BF = AB - AF$
$ = 13 - 7$
Let us subtracting the terms
$ = 6{\text{cm}}$
Also we can see in the diagram clearly that $BC = CD + BD$
Now we have to find out $CD$, we can write it as,
$CD = BC - BD$
$ = 14 - 6$
On subtracting the terms we get,
$ = 8{\text{cm}}$
Since, we already know that the tangents of the circle
$CE = CD = 8cm$
We required the length of $AC$
$AC = AE + EC$
Substitute the value of $AE$ and $EC$ we get,
$ = 7 + 8$
On adding the terms we get,
$ = 15{\text{cm}}$
$\therefore $Hence we attained the required result.

That is $AC = 15cm$.

Note: The students might forget to write the units at the end, but without units we cannot talk about the concept of length.
Because writing just $10$ does not make any sense, but $10{\text{cm}}$ does make sense.
The student might think that ${\text{D, E and F}}$ are the midpoints but that is not necessary and you cannot put that argument without any solid reason as well.