Question

In circular motion at a given instant centripetal acceleration is $3\dfrac{{cm}}{{{s^2}}}$ and the angle between the resultant acceleration and centripetal acceleration is ${45^ \circ }$. At that instant the magnitude of the resultant acceleration is:
A) $3\dfrac{{cm}}{{{s^2}}}$
B) $4.2\dfrac{{cm}}{{{s^2}}}$
C) $1.2\dfrac{{cm}}{{{s^2}}}$
D) $2.8\dfrac{{cm}}{{{s^2}}}$

Answer 1

Hint- As, angle between the resultant acceleration and the centripetal acceleration is ${45^ \circ }$, therefore the angle between the resultant acceleration and the tangential acceleration is ${45^ \circ }$also since centripetal acceleration and tangential acceleration are perpendicular.

Formula used: \[{a_r}\cos \theta = {a_c}\]
Where, \[{a_r} = \]The resultant acceleration
\[{a_c} = \]The centripetal acceleration
θ= The angle between the resultant acceleration and the centripetal acceleration.

Complete step by step answer:
When an object is moving along a circular path, it has an acceleration along the radius towards the center of the circle or the circular path. This centralized acceleration is called centripetal acceleration.
Here given a resultant acceleration say \[{a_r}\] and a centripetal acceleration say \[{a_c} = 3\dfrac{{cm}}{{{s^2}}}\].
And, the angle between the resultant acceleration and the centripetal acceleration is given ${45^ \circ }$.
So, we may conclude that there must be an acceleration that exists towards the tangent along the radius at which the centripetal acceleration is working.
We may show the above assumption by a simple diagram,

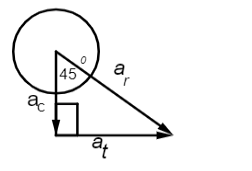
\[{a_r} = \]The resultant acceleration
\[{a_c} = \]The centripetal acceleration
\[{a_t} = \]The tangential acceleration.
Hence, the centripetal acceleration and the tangential acceleration are two components of the resultant acceleration.
So, if we divide the Resultant vector into two components at angle $\theta $ (given\[\theta = {45^0}\]) represented by the below diagram,

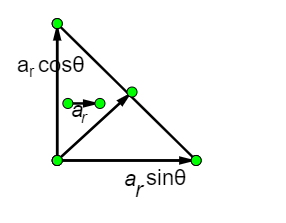
we can write, \[{a_r}\cos \theta = {a_c}\]
and, \[{a_r}\sin \theta = {a_t}\]
so, \[{a_r}\cos \theta = {a_c}\]

\[ \Rightarrow {a_r} = \dfrac{3}{{\cos {{45}^0}}}[\because {a_c} = 3,\theta = {45^0}]\]

\[ \Rightarrow {a_r} = \dfrac{3}{{\dfrac{1}{{\sqrt 2 }}}}\]
 \[ \Rightarrow {a_r} = 3 \times \sqrt 2 \]
 \[ \Rightarrow {a_r} = 4.24\]
Therefore the magnitude of the resultant is $4.2\dfrac{{cm}}{{{s^2}}}$.

Hence the option (B) is the right answer.

Notes: The centripetal acceleration acts towards the center of the circular path along the radius of the circle. Since the tangent and the radius of a circle is perpendicular to each other hence the tangential acceleration and centripetal acceleration are also perpendicular to each other.
The velocity of the object moving along a circular path always acts towards the tangent corresponding to the radius of the circle. Hence, the velocity is always perpendicular to the centripetal acceleration.