
In circle $O$, $\overline{AOB}\bot \overline{COD}$. Find m arc $AC$ and m arc $ADC$.

Answer
611.1k+ views
Hint: To find m arc $AC$ and m arc $ADC$, we have to find the angle subtended by the arc $AC$ and the arc $ADC$ on the centre of the circle. To find this angle, we will use the information given in the question i.e. $\overline{AOB}\bot \overline{COD}$.
Complete step by step answer:
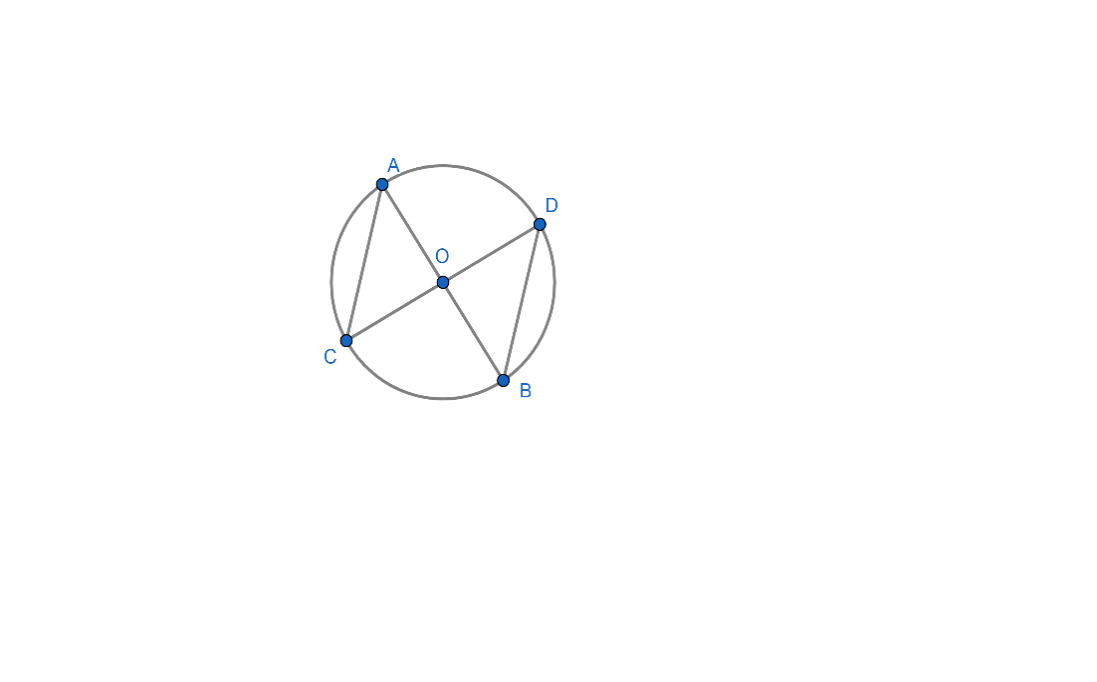
It is given in the question that $\overline{AOB}\bot \overline{COD}$ and $A,B,C,D$ lies on the circumference of the circle which has its centre at point $O$.
Let us consider the figure given in the question,
Since it is given that $\overline{AOB}\bot \overline{COD}$, we get
$\angle AOC=\angle AOD=\angle DOB=\angle BOC={{90}^{\circ }}................\left( i \right)$
In the question, we are required to find m arc $AC$.
We know that m arc $AC$ is a representation of degree measure of arc $AC$. This states that the degree measure m arc $AC$ = $\angle AOC$.
From $\left( i \right)$ , we have
$\angle AOC={{90}^{\circ }}$
So, we get the degree measure of arc $AC={{90}^{\circ }}$.
Hence, we obtain m arc $AC$ = ${{90}^{\circ }}$.
In the question, we are also required to find m arc $ADC$.
m arc $ADC$represents the degree measure of arc $ADC$.
Degree measure of $ADC$ will be equal to the sum of degree measure of arc $AOD$, arc $DOB$ and arc $BOC$. This means m arc $ADC$ can be given by
m arc $ADC$ = $\angle AOD+\angle DOB+\angle BOC...............\left( ii \right)$
From equation $\left( i \right)$, we have
$\angle AOD=\angle DOB=\angle BOC={{90}^{\circ }}$
Substituting $\angle AOD=\angle DOB=\angle BOC={{90}^{\circ }}$ from equation $\left( i \right)$ in equation $\left( ii \right)$, we get
m arc $ADC$ = ${{90}^{\circ }}+{{90}^{\circ }}+{{90}^{\circ }}$.
Hence, we have m arc $ADC$ = ${{270}^{\circ }}$.
So, the degree measures of the arcs $AC$ and $ADC$ are obtained as m arc $AC$ = ${{90}^{\circ }}$ and m arc $ADC$ = ${{270}^{\circ }}$.
Note: There is a possibility that one might make a mistake while calculating m arc $AC$. One may find out m arc $AC$ as the angle subtended by the major arc $AC$ on the centre of the circle. But since nothing is mentioned in the question, by default, one might consider m arc $AC$ as the angle subtended by the minor arc $AC$ on the centre of the circle.
Complete step by step answer:
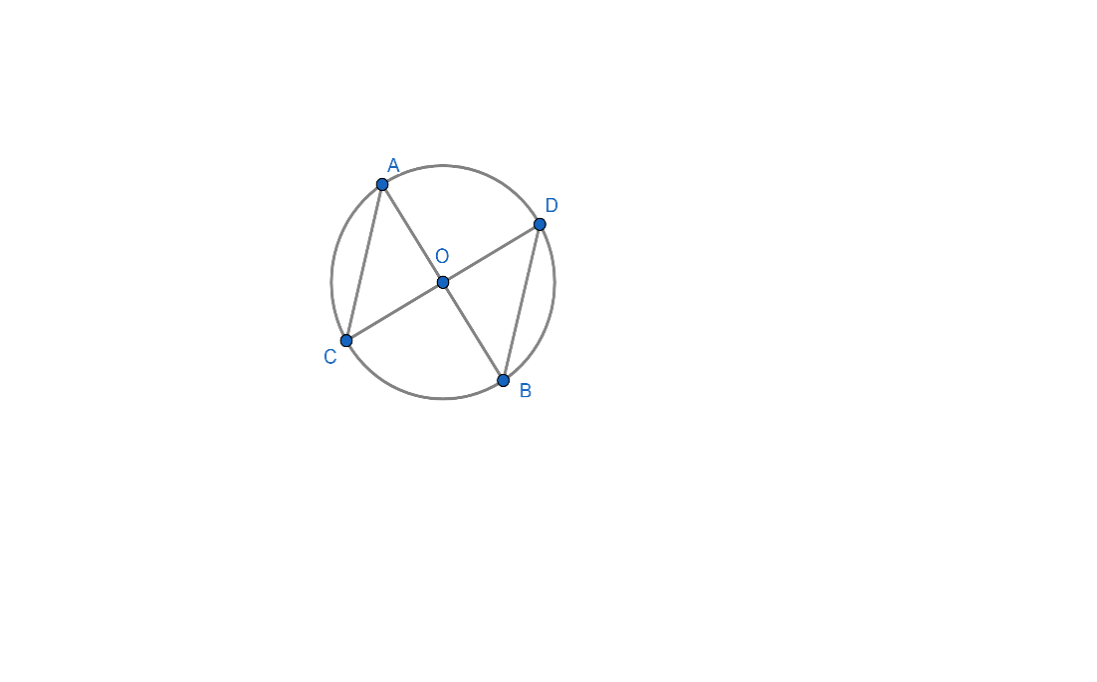
It is given in the question that $\overline{AOB}\bot \overline{COD}$ and $A,B,C,D$ lies on the circumference of the circle which has its centre at point $O$.
Let us consider the figure given in the question,

Since it is given that $\overline{AOB}\bot \overline{COD}$, we get
$\angle AOC=\angle AOD=\angle DOB=\angle BOC={{90}^{\circ }}................\left( i \right)$
In the question, we are required to find m arc $AC$.
We know that m arc $AC$ is a representation of degree measure of arc $AC$. This states that the degree measure m arc $AC$ = $\angle AOC$.
From $\left( i \right)$ , we have
$\angle AOC={{90}^{\circ }}$
So, we get the degree measure of arc $AC={{90}^{\circ }}$.
Hence, we obtain m arc $AC$ = ${{90}^{\circ }}$.
In the question, we are also required to find m arc $ADC$.
m arc $ADC$represents the degree measure of arc $ADC$.
Degree measure of $ADC$ will be equal to the sum of degree measure of arc $AOD$, arc $DOB$ and arc $BOC$. This means m arc $ADC$ can be given by
m arc $ADC$ = $\angle AOD+\angle DOB+\angle BOC...............\left( ii \right)$
From equation $\left( i \right)$, we have
$\angle AOD=\angle DOB=\angle BOC={{90}^{\circ }}$
Substituting $\angle AOD=\angle DOB=\angle BOC={{90}^{\circ }}$ from equation $\left( i \right)$ in equation $\left( ii \right)$, we get
m arc $ADC$ = ${{90}^{\circ }}+{{90}^{\circ }}+{{90}^{\circ }}$.
Hence, we have m arc $ADC$ = ${{270}^{\circ }}$.
So, the degree measures of the arcs $AC$ and $ADC$ are obtained as m arc $AC$ = ${{90}^{\circ }}$ and m arc $ADC$ = ${{270}^{\circ }}$.
Note: There is a possibility that one might make a mistake while calculating m arc $AC$. One may find out m arc $AC$ as the angle subtended by the major arc $AC$ on the centre of the circle. But since nothing is mentioned in the question, by default, one might consider m arc $AC$ as the angle subtended by the minor arc $AC$ on the centre of the circle.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




