Question

In Bohr’s atomic model, radius and energy in orbit (n) is related as:
A. $r \propto {n^2}$, $E \propto \dfrac{1}{{{n^2}}}$
B. $r \propto \dfrac{1}{{{n^2}}}$, $E \propto {n^2}$
C. $r \propto \dfrac{1}{n}$, $E \propto n$
D. $E \propto {n^2}$, $r \propto {n^2}$

Answer 1

Hint: Rutherford explained that the nucleus is surrounded by negatively charged electrons. We know that Bohr’s atomic model was proposed by Neil Bohr in the year 1815 after Rutherford’s nuclear model of the atom. Bohr’s model explained that the nucleus is in the center which is positively charged and is surrounded by negatively charged particles called electrons that move around the nucleus in a fixed orbital. Electrons revolve around the nucleus in fixed circular orbitals known as shells and each orbital has fixed energy. The orbitals 1, 2, 3, 4…. are K, L, M, N... respectively. When electrons in a high energy orbital are moved to lower energy orbital by losing energy as shown in the figure and gain energy in the vice versa.

Complete answer: or Complete step by step answer:

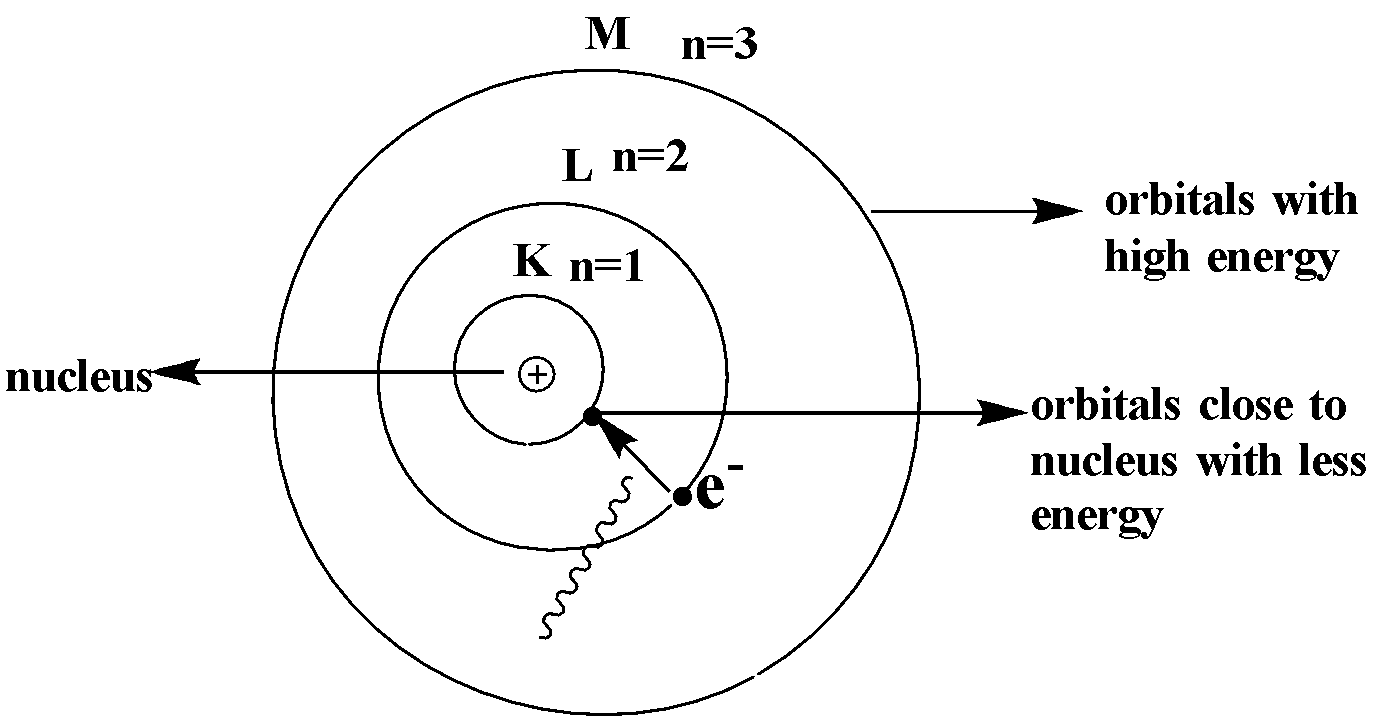
In Bohr’s model, we are considering a hydrogen atom. We can find out the energy and radius of any orbit using Bohr’s model of an atom.
Consider an atom with atomic number Z which electron is in ${n^{th}}$ orbit.
According to Bohr’s postulates, we know that the electrostatic force by the electrons in an orbit to the nucleus provides the centripetal force, which is the force that acts on an object to keep it moving in a circular orbit.
So we can say electrostatic force and centripetal force are equal.
$\dfrac{1}{{4\pi {E_0}}} \times \dfrac{{z{e^2}}}{{{r^2}}} = \dfrac{{m{v^2}}}{r}$z is the charge, r is the radius or distance from the nucleus to the orbit, m is the mass, e is the electron charge.
On rearranging, ${v^2} = \dfrac{1}{{4\pi {E_0}}} \times \dfrac{{z{e^2}}}{{mr}} \to (1)$
We know that angular momentum, $L = mvr = n\lambda = \dfrac{{nh}}{{2\pi }}$
$\lambda $ is the wavelength.
From the above equation, $v = \dfrac{{nh}}{{mr}}$
Substituting this in equation 1, we get $\dfrac{{{n^2}{h^2}}}{{{m^2}{r^2}}} = \dfrac{1}{{4\pi {E_0}}} \times \dfrac{{z{e^2}}}{{mr}}$
$ \Rightarrow r = \dfrac{{4\pi {E_0}{n^2}{h^2}}}{{mz{e^2}}}$
So we can say that $r \propto {n^2}$ radius is directly proportional to the square of the orbital number.
Now we got the radius of the ${n^{th}}$orbital.
Let us now find the energy of an electron in an orbit.
The total energy of an electron in an orbit is the sum of the kinetic energy of the electron due to its movement around the nucleus and the potential energy which is due to the interaction between the positively charged nucleus and electron.
Potential Energy $ = \dfrac{{ - kz{e^2}}}{r}$
$k \times \dfrac{{z{e^2}}}{{{r^2}}} = \dfrac{{m{v^2}}}{r}$
$ \Rightarrow k \times \dfrac{{z{e^2}}}{r} = m{v^2}$
We know that $kinetic\; energy = \dfrac{{m{v^2}}}{2}$
So here $\dfrac{{m{v^2}}}{2} = \dfrac{{kz{e^2}}}{{2r}}$
Net energy is the sum of potential energy and kinetic energy.
${E_n} = K.E + P.E$
$ \Rightarrow {E_n} = \dfrac{{kz{e^2}}}{{2r}} + \dfrac{{ - kz{e^2}}}{r}$
$ \Rightarrow {E_n} = - \dfrac{{kz{e^2}}}{{2r}}$
Substituting the value of r in the above equation, we get ${E_n} = \dfrac{{ - kz{e^2}mz{e^2}}}{{2k{n^2}{h^2}}}$
So we can say that ${E_n} \propto \dfrac{1}{{{n^2}}}$

So, the correct answer is Option A .

Note:
Bohr model does not explain the Zeeman effect and the Stark effect. It violates the Heisenberg Uncertainty Principle. The Bohr atomic model theory made correct predictions for smaller sized atoms like hydrogen, but when larger atoms are considered poor, spectral predictions are obtained.