Question

In any triangle ABC if $a\cos A=b\cos B$, then the triangle is either isosceles or right-angled triangle.
A. True
B. False

Answer 1

Hint: Construct a triangle AB and use cosine law along with the information provided in the question. From this we will come to see that the triangle can be either an isosceles or a right angled triangle or both.

Complete step by step answer:
Let the triangle b triangle ABC ,

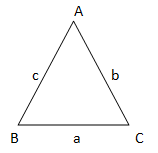
Formula used: Cosine law
$\cos A=\left( \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \right)$ …..(1)
$\cos B=\left( \dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac} \right)$ .…..(2)

Now, as given in question
            $a\cos A=b\cos B$
Now, using (1) and (2), we get;
$a\left( \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \right)=b\left( \dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac} \right)$
Now, we cancel out $2$and $c$ because $c\ne 0$
 $a\left( \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{b} \right)=b\left( \dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{a} \right)$
Now, we multiply $ab$on both sides, we get;
${{a}^{2}}\left( {{b}^{2}}+{{c}^{2}}-{{a}^{2}} \right)={{b}^{2}}\left( {{a}^{2}}+{{c}^{2}}-{{b}^{2}} \right)$
$\Rightarrow {{a}^{2}}{{b}^{2}}+{{a}^{2}}{{c}^{2}}-{{a}^{4}}={{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}-{{b}^{4}}$
\[\Rightarrow \left( {{a}^{2}}{{b}^{2}}+{{b}^{4}}-{{b}^{2}}{{c}^{2}} \right)+\left( {{a}^{2}}{{c}^{2}}-{{a}^{4}}-{{a}^{2}}{{b}^{2}} \right)=0\]
$\Rightarrow {{b}^{2}}\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)+{{a}^{2}}\left( {{c}^{2}}-{{a}^{2}}-{{b}^{2}} \right)=0$
$\Rightarrow {{b}^{2}}\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)-{{a}^{2}}\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)=0$
$\Rightarrow \left( {{b}^{2}}-{{a}^{2}} \right)\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)=0$
 Now, we see that,
$\Rightarrow \left( {{b}^{2}}-{{a}^{2}} \right)\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)=0$
So, either ${{b}^{2}}-{{a}^{2}}=0$
Or ${{a}^{2}}+{{b}^{2}}-{{c}^{2}}=0$ or both
Case – 1st
So, first we assume ${{b}^{2}}-{{a}^{2}}=0$and ${{a}^{2}}+{{b}^{2}}-{{c}^{2}}\ne 0$
Then,
${{b}^{2}}-{{a}^{2}}=0$
$\Rightarrow \left( b-a \right)\left( b+a \right)=0$
Now, since $b$and $a$ are sides of a triangle
So, $b$and $a$ could not be equal to zero
So, $\left( b+a \right)\ne 0$
Hence, $b-a=0$ $\Rightarrow b=a$
This means side AC and BC are of same length. Hence, in this case triangle can be isosceles.

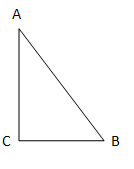
Case – 2nd
Now, we assume ${{a}^{2}}+{{b}^{2}}-{{c}^{2}}=0$ and ${{b}^{2}}-{{a}^{2}}\ne 0$
So,
${{a}^{2}}+{{b}^{2}}-{{c}^{2}}$
$\Rightarrow {{a}^{2}}+{{b}^{2}}={{c}^{2}}$
But, if ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$ that means triangle ABC is right angled triangle at C by Pythagoras theorem.
So, triangle ABC is right angled triangle at C.
Case – 3rd
Both are zero
So, in this case the triangle ABC is both isosceles and right angled triangle.
So, from the three cases we conclude that for given condition in question the triangle should be either isosceles or right angled triangle or both.
Therefore, the given statement in the question is true.
Hence, the correct option is (A).

NOTE: One may start solving by using sine law but this on the other hand will lead to rather unnecessary cumbersome calculation, which should be avoided.