Question

In an isosceles triangle, the vertex angle is twice the sum of the base angles. Find the angles of the triangle.

Answer 1

Hint:
Let's know about the isosceles triangle and it’s property.
 In an isosceles triangle, the length of two sides are equal.

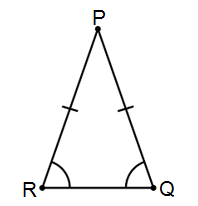
In isosceles triangle,\[\vartriangle {\text{PQR}}\], PR = PQ,
Hence, base angles, $\angle {\text{PRQ }} = {\text{ }}\angle {\text{PQR}}$, ($\because $angles opposite to equal sides are equal)
Angle sum property of triangle: the sum of all interior angles of a triangle is equal to $180^\circ $.
Hence, In \[\vartriangle {\text{PQR}}\](Figure 1:) , $\angle {\text{PRQ + }}\angle {\text{PQR + }}\angle {\text{RPQ = 180}}^\circ $
Form the mathematical equations as stated in the language of question.
The word ‘twice’ implies the multiplication by ‘2’, similarly, ‘two times’ also implies multiplication by ‘2’.
Base angles in isosceles triangles are the angles opposite to the equal sides of the triangles. Angle formed by equal sides of the isosceles triangle is known as the Vertex angle.

Complete step by step solution:
Step 1: Draw the given figure

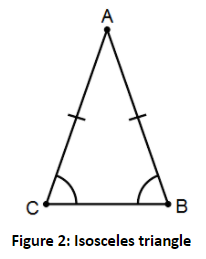
Step 2: given that \[\vartriangle {\text{ABC}}\] is an isosceles triangle
Thus, by property of isosceles triangle, two sides are equal
AB = AC, …… (1)
$ \Rightarrow $angles opposite to equal sides are equal:
Angle opposite to the side AC = $\angle {\text{ABC }}$
Angle opposite to the side AB = $\angle {\text{ACB }}$
Hence, base angles, $\angle {\text{ABC }} = {\text{ }}\angle {\text{ACB}}$, ($\because $angles opposite to equal sides are equal) …… (2)
Step 3: apply the given condition i.e.
vertex angle ( $\angle {\text{BAC}}$), is twice the sum of the base angles
     \[\angle {\text{BAC = 2(}}\angle {\text{ABC + }}\angle {\text{ACB)}}\]
\[ \Rightarrow \angle {\text{BAC = 2(}}\angle {\text{ACB + }}\angle {\text{ACB)}}\] (from (2))
\[ \Rightarrow \angle {\text{BAC = 2(2}} \times \angle {\text{ACB)}}\]
\[ \Rightarrow \angle {\text{BAC = 4(}}\angle {\text{ACB)}}\] …… (3)
Step 5: angle sum property of a triangle:
In \[\vartriangle {\text{ABC}}\],
    $\angle {\text{ABC + }}\angle {\text{BCA + }}\angle {\text{CAB = 180}}^\circ $
$\angle {\text{ACB + }}\angle {\text{ACB + 4(}}\angle {\text{ACB}}){\text{ = 180}}^\circ $ (from (2) and (3))
\[
   \Rightarrow {\text{ 6(}}\angle {\text{ACB}}){\text{ = 180}}^\circ \\
   \Rightarrow {\text{ }}\angle {\text{ACB = }}\dfrac{{{\text{180}}^\circ }}{6} \\
 \]
\[ \Rightarrow {\text{ }}\angle {\text{ACB = 30}}^\circ \] …… (4)
Step 6: by help of \[{\text{ }}\angle {\text{ACB = 30}}^\circ \] evaluate other angles
$\angle {\text{ABC }} = {\text{ }}\angle {\text{ACB = 30}}^\circ $
\[
  \angle {\text{BAC = 4(}}\angle {\text{ACB) = 4}} \times {\text{30}}^\circ \\
  {\text{ = 120}}^\circ \\
 \]
The angles of isosceles triangle are $\angle {\text{ABC = 30}}^\circ ,{\text{ }}\angle {\text{BCA = 30}}^\circ ,{\text{ }}\angle {\text{CAB = 120}}^\circ $.

Additional information: In equilateral triangle, all three sides are equal in length.

In the scalene triangle, all the three sides are different (or unequal) in length.

Note:
The area of a triangle is equal to the half of multiplication of base and height.
Area $\vartriangle = \dfrac{1}{2} \times base \times height$
Here, base is that side of the triangle on which height is drawn.
Perimeter of a triangle is equal to the sum of the length of all three sides of the triangle.