Question

In an isosceles trapezoid \[ABCD\], \[AB = CD = 5\]. The top base \[ = 8\] and the bottom base \[ = 14\]. What is the area of this trapezoid?

Answer 1

Hint: We will first extract a rectangle from the center section of the isosceles trapezoid \[ABCD\] which will leave two right angled triangles. In this right-angled triangle, using the Pythagoras theorem we will find the height of the trapezoid. As we know that \[{\text{area of a trapezoid}} = \left( {\dfrac{{{\text{base}} + {\text{top}}}}{2}} \right) \times {\text{height}}\], using this formula we will find the area of this trapezoid.

Complete step by step answer:

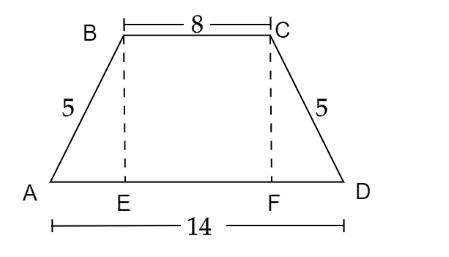
Given, an isosceles trapezoid \[ABCD\] where \[AB = CD = 5\]. The top base \[ = 8\] and the bottom base \[ = 14\]. If we extract a rectangle \[BCFE\] from the center section of the isosceles trapezoid \[ABCD\], then two right angled triangles \[\vartriangle ABE\] and \[\vartriangle DCF\] will be left. In rectangle \[BCFE\], \[BC = EF = 8\]. As we know that base angles of an isosceles trapezoid are equal in measure i.e., \[\angle BAE = \angle CDF\], let’s say equal to \[x\]. As we know, the sum of all the angles in a triangle is equal to \[{180^ \circ }\]. Therefore, in \[\vartriangle ABE\] and \[\vartriangle DCF\], we have
\[ \Rightarrow \angle AEB + \angle EBA + \angle BAE = {180^ \circ }\] and \[\angle DFC + \angle FCD + \angle CDF = {180^ \circ }\]
\[ \Rightarrow {90^ \circ } + \angle EBA + x = {180^ \circ }\] and \[{90^ \circ } + \angle FCD + x = {180^ \circ }\]

On simplifying, we get \[\angle EBA = \angle FCD = {90^ \circ } - x\]
In \[\vartriangle ABE\] and \[\vartriangle DCF\],
\[\Rightarrow AB = DC\]...........(given)
\[\Rightarrow \angle EBA = \angle FCD\]..............(Proved above)
\[\Rightarrow BE = CF\]..............(Opposite sides of a rectangle)
Therefore, by side-angle-side, \[\vartriangle ABE \cong \vartriangle DCF\].So, we get \[AE = FD\], let’s say \[a\]. We have \[AE + EF + FD = 14\]
\[ \Rightarrow a + 8 + a = 14\]
On simplification, we get
\[ \Rightarrow a = 3\]
\[\therefore AE = FD = 3\]
In \[\vartriangle ABE\], using Pythagoras theorem we have
\[ \Rightarrow A{B^2} = B{E^2} + A{E^2}\]

Putting the values, we get
\[ \Rightarrow {\left( 5 \right)^2} = B{E^2} + {\left( 3 \right)^2}\]
\[ \Rightarrow 25 = B{E^2} + 9\]
Subtracting \[9\] from both the sides and on rewriting, we get
\[ \Rightarrow B{E^2} = 25 - 9\]
\[ \Rightarrow B{E^2} = 16\]
Taking square root both sides, we get
\[ \Rightarrow BE = \pm 4\]
But distance can’t be negative. So, \[BE \ne - 4\].
Therefore, \[BE = 4\].
In a similar way, we get \[CF = 4\].
Therefore, we get \[{\text{height}} = 4\].

Now, as we know that,
\[{\text{area of a trapezoid}} = \left( {\dfrac{{{\text{base}} + {\text{top}}}}{2}} \right) \times {\text{height}}\]
Here, \[{\text{base}} = 14\], \[{\text{top}} = 8\] and \[{\text{height}} = 4\].
Using this, we get
\[ \Rightarrow {\text{area of a trapezoid}} = \left( {\dfrac{{{\text{14}} + {\text{8}}}}{2}} \right) \times {\text{4}}\]
\[ \Rightarrow {\text{area of a trapezoid}} = \dfrac{{22}}{2} \times {\text{4}}\]
On simplification, we get
\[ \therefore {\text{area of a trapezoid}} = 44\]

Therefore, the area of this trapezoid is \[44\].

Note: Isosceles trapezoid is a special case of trapezoid. In isosceles trapezoids, the diagonals are equal in length. Also, rectangles and squares are usually considered to be special cases of isosceles trapezoids. A non-rectangular parallelogram is not an isosceles trapezoid because it has no line of symmetry.