Question

In an isosceles trapezium diagonal is inclined at angle ${45^ \circ }$ with the parallel sides. The height of the trapezium is $12\,cm$. How will you find out the area of the trapezium without using trigonometry?

Answer 1

Hint: Here in this question, we have to find the area of isosceles trapezium, For this, first we need to draw a figure according to given data and note down the values of each side then substitute and simplify by using a formula of area of trapezium to get the required solution.

Complete step by step answer:
A trapezoid, also known as a one type of quadrilateral, which is a flat closed shape having 4 straight sides, with one pair of parallel sides. The parallel sides of a trapezium are known as the bases, and its non-parallel sides are called legs.Isosceles trapezoid is a trapezoid with its two nonparallel sides equal.The area of a triangle is defined as the total region that is enclosed by the trapezium.

Area of a trapezoid is found with the formula:
Area$ = $(sum of parallel sides $ \div $ 2) $ \times $ height.
i.e., $Area = \left( {\dfrac{{a + b}}{2}} \right) \times h$.
Now, consider a given question: Let us consider trapezium $ABCD$, side AB is parallel to CD ($AB\parallel CD$), A is inclines at the angle ${45^ \circ }$ from point D, height of the trapezium $AE = BF = 12\,cm$.

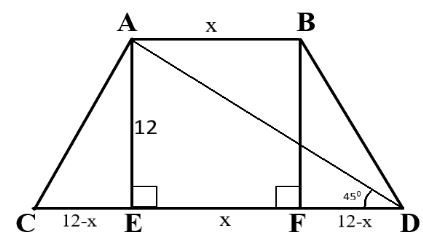
From the figure, the angle $\angle ADE = {45^ \circ }$, and the height $AE = 12$, $ \Rightarrow ED = 12$
Similarly, $BF = 12, \Rightarrow CF = 12$

Let us take, $AB = x$ and $EF = x$, then
$FD = 12 - x$ and $CE = 12 - x$.
$ \Rightarrow \,\,CD = CE + EF + FD$
$ \Rightarrow \,\,CD = \left( {12 - x} \right) + x + \left( {12 - x} \right)$
$ \Rightarrow \,\,CD = 12 - x + x + 12 - x$
On simplification, we get
$ \Rightarrow \,\,CD = 24 - x$

Now, consider the area of trapezium
$ \Rightarrow \,\,\,\,Area = \left( {\dfrac{{AB + CD}}{2}} \right) \times AE$
$ \Rightarrow \,\,\,\,Area = \left( {\dfrac{{x + 24 - x}}{2}} \right) \times 12$
$ \Rightarrow \,\,\,\,Area = \left( {\dfrac{{24}}{2}} \right) \times 12$
$ \Rightarrow \,\,\,\,Area = 12 \times 12$
$\therefore \,\,\,\,Area = 144\,\,c{m^2}$ cm.

Hence, the area of trapezium $144\,\,cm$.

Note: While determining the area we use the formula. The formula is $Area = \left( {\dfrac{{a + b}}{2}} \right) \times h$. The unit for the perimeter will be the same as the unit of the length of a side or triangle. Whereas the unit for the area will be the square of the unit of the length of a triangle. We should not forget to write the unit.