Question

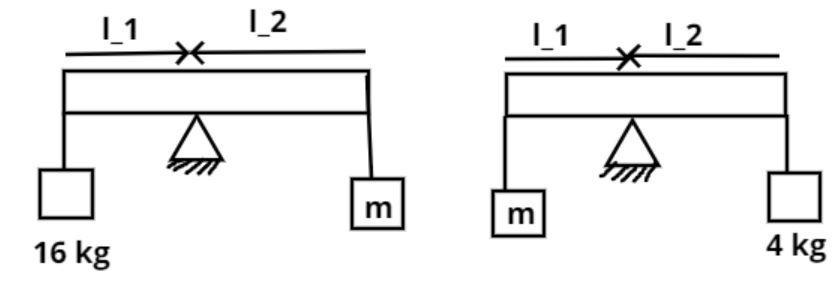
In an experiment with a beam balance, an unknown mass m is balanced by two known masses of 16 kg and 4 kg as shown in figure find m.

$\left( A \right)10kg$
$\left( B \right)6kg$
$\left( C \right)8kg$
$\left( D \right)12kg$

Answer 1

Hint: In this question use the concept of equilibrium (i.e. at balance) so at the equilibrium mass multiplied by respective length is always equal to another mass multiplied by respective length of this mass that is from balance point so use these concepts to reach the solution of the question.

Formula used:
${m_1}{l_1} = {m_2}{l_2}$

Complete step by step answer:
After balancing the beam the beam kept in horizontal position as shown in the figure and made a straight angle i.e. 180 degree with the horizontal.
To make the balance we kept the beam at a certain point such that the known weight and the unknown weight balances each other w.r.t the length from the balance point.
It is given that an unknown mass m is balanced by two known masses of 16 kg and 4 kg as shown in figure.
So at balance known mass multiplied by the respective side length from the balance point is equal to unknown mass multiplied by respective side length from the balance point.
Let, ${m_1} = 16kg,{m_2} = m,{m_3} = 4kg$
From figure (1) we have,
$ \Rightarrow {m_1}{l_1} = {m_2}{l_2}$
$ \Rightarrow \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{{l_2}}}{{{l_1}}}$.................. (1)
And from figure (2) we have,
$ \Rightarrow {m_2}{l_1} = {m_3}{l_2}$
$ \Rightarrow \dfrac{{{m_2}}}{{{m_3}}} = \dfrac{{{l_2}}}{{{l_1}}}$.................. (2)
So from equation (2) and (3) we have,
$ \Rightarrow \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{{m_2}}}{{{m_3}}}$
Now substitute the values we have,
$ \Rightarrow \dfrac{{16}}{m} = \dfrac{m}{4}$
$ \Rightarrow {m^2} = 64$
Now take square root on both sides we have,
$ \Rightarrow \sqrt {{m^2}} = \sqrt {64} $
$ \Rightarrow m = \sqrt {8 \times 8} $
$ \Rightarrow m = 8kg$
So this is the required answer.
Hence option (C) is the correct answer.

Note:
Whenever we face such types of questions always recall the property that at balance or at equilibrium the mass multiply by the respective side length from the balance point is equal to unknown mass multiply by respective side length from the balance point so just equate them for both the figures as above and simplify, we will get the required unknown mass.