Question

In an experiment, a small steel ball falls through a liquid at a constant speed of $10cm{{s}^{-1}}$. If the steel ball is pulled upward with a force which is equivalent to twice of its effective weight, how fast will it move upward?
$\begin{align}
  & A.5cm{{s}^{-1}} \\
 & B.0cm{{s}^{-1}} \\
 & C.10cm{{s}^{-1}} \\
 & D.20cm{{s}^{-1}} \\
\end{align}$

Answer 1

Hint: In order to find the effective weight, draw the diagram showing all the forces acting on the steel balls. Then apply the condition where the steel ball is pushed upwards with a force equal to the double of the effective weight. For this also draw a diagram showing the forces acting. These details may help you to solve this question.

Complete step-by-step answer:
First of all let us take the journey of a steel ball through the liquid mentioned in the first part of the question with a constant speed of $10cm{{s}^{-1}}$. Let is draw the diagram in which all the force acting on the steel ball is being shown.

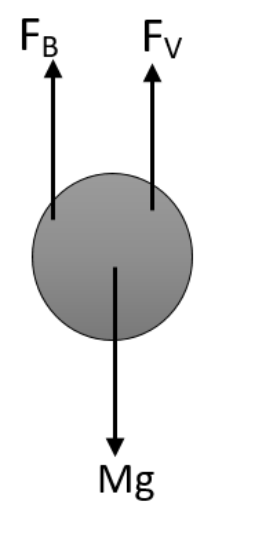
Therefore the effective weight is given as,
${{W}_{effective}}=mg-{{F}_{B}}$

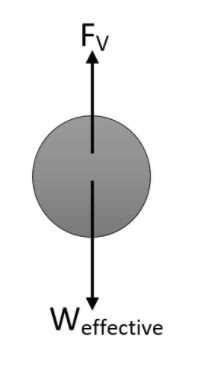
Now let us look at what happens when the force equal to the twice of the effective weight is applied in the upward direction. Let us show this also using the diagram,

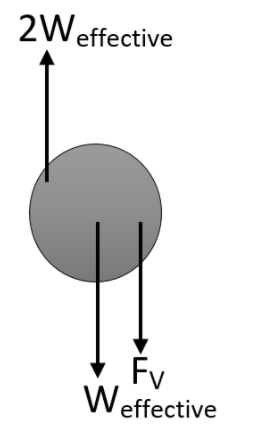
The resultant of the effective weight will be,
$2{{W}_{\text{effective}}}-{{W}_{\text{effective}}}={{W}_{\text{effective}}}$

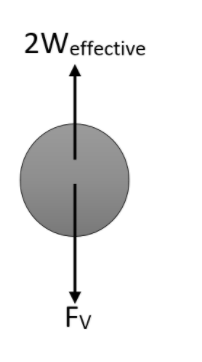
Therefore we can write that the effective weight in resultant is the same and it is acting opposite to the viscous force also. This was the same condition in the above cases also where the only difference is in the direction of motion of the steel ball. In the first case the ball was moving downwards and in second case the ball was moving upwards because of the force acting on it.
Therefore the speed of the ball will be the same in the upward direction.
$v=10m{{s}^{-1}}$
Therefore the correct answer is option C.

Note: Viscous force can be considered similar to the force of friction. Only small differences are there. Viscous force is the opposition for a body which is moving in a fluid which will prevent the motion between the two layers of a flowing fluid.