Question

In an equilateral triangle with side ‘a’. Prove that the area of the triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$.

Answer 1

Hint: Here, we draw the figure of the equilateral triangle with side a and also draw its height by taking any side as the base. Then find the height of the triangle using the Pythagoras theorem. Then apply the formula of area of the triangle, in this way we can prove. Also, there will be only one variable that is side.

Complete step by step solution:
Construction: Let triangle $ABC$ is an equilateral triangle drawn below.
In a triangle $ABC$,
$AB = BC = AC = a$

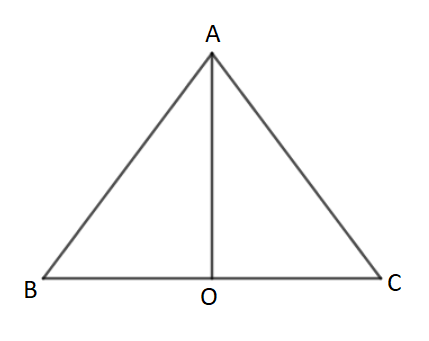
Now, we will draw a line AO which bisects the side BC at O.
$BO = OC = \dfrac{a}{2}$
We have;
BO = $\dfrac{a}{2}$, AB = a
In triangle ABO,
Using Pythagoras theorem,
$A{O^2} + B{O^2} = A{B^2}$\[\]
[Pythagoras Theorem states that, in an right angled triangle sum of squares of two sides is equal to the square of the hypotenuse]
$ \Rightarrow A{O^2} + {\left( {\dfrac{a}{2}} \right)^2} = {a^2}$
$ \Rightarrow A{O^2} = {a^2} - \dfrac{{{a^2}}}{4}$
$ \Rightarrow AO = \sqrt {\dfrac{{3{a^2}}}{4}} = \dfrac{{\sqrt 3 }}{2}a$.
Now, we will find the area of a triangle ABC, where AO is height and BC is base.
Area of a triangle ABC $ = \dfrac{1}{2} \times base \times height$
$ = \dfrac{1}{2} \times a \times \dfrac{{\sqrt 3 a}}{2} = \dfrac{{\sqrt 3 }}{4}{a^2}$

$\therefore$ It is proved that the area of a triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$.

Note:
As we know that, the Area of a triangle is $\dfrac{1}{2} \times base \times height$ but the area of an equilateral triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$, where a is the sides of an equilateral triangle. To prove these types of formulas use simple methods only. Also, you can use this formula directly. These three types of triangles which are scalene triangles, equilateral triangles, and isosceles triangles. An equilateral triangle has all the three sides equal and all angles equal to ${60^ \circ }$. All the angles in an equilateral triangle are congruent. The area of an equilateral triangle is the amount of space occupied by an equilateral triangle.