Question

In an equilateral triangle of side 24cm, a circle is inscribed touching its sides. Find the area of the remaining portion of the triangle. [Take \[\sqrt{3}=1.732\]].
(a) \[68.21c{{m}^{2}}\]
(b) \[98.55c{{m}^{2}}\]
(c) \[112.67c{{m}^{2}}\]
(d) \[154.12c{{m}^{2}}\]

Answer 1

Hint: Draw a diagram of an equilateral triangle with a circle inscribed in it. Construct a line joining one of the vertices of the triangle with the centre of the circle. Assuming this line to be angle bisector determine the value of radius of the circle by using the formula: - \[\tan \theta =\dfrac{r}{\left( \dfrac{a}{2} \right)}\], where \[\theta ={{30}^{\circ }}\], r = radius of circle and a = 24cm. Now, subtract the area of the circle from the area of the triangle to get the area of the remaining portion. Use the formulas: - Area of circle = \[\pi {{r}^{2}}\], Area of an equilateral triangle = \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\].

Complete step by step answer:
Here, we have been provided with an equilateral triangle with a circle inscribed in it touching its sides. So, let us draw a diagram for the given condition.

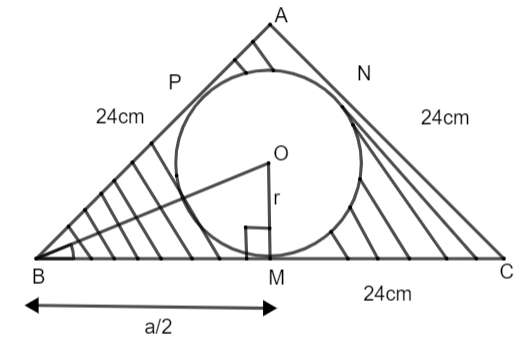
In the above figure we have assumed an equilateral triangle ABC with each side equal to 24cm. A circle with centre O is inscribed in the triangle such that it touches sides AB, BC and CA at P, M and N respectively.
Now, we have constructed a line joining vertex B and centre O and we have also joined OM such that it is the radius (r) of the circle.
We know that, in an equilateral triangle, angle bisectors, medians, perpendicular bisectors, incentre all lie on the same line. Therefore, OB is the angle bisector of angle B. Here, BC is behaving like a tangent to the circle and we know that “line joining the centre of the circle to the tangent that is radius, is perpendicular to the tangent”. So, OM is perpendicular to BC. Hence, OMB is a right angle triangle.
Now, in triangle OMB, we have,
\[\Rightarrow \angle OBM=\dfrac{1}{2}\times \angle B=\dfrac{1}{2}\times {{60}^{\circ }}={{30}^{\circ }}\]
\[\Rightarrow \] OM = radius = r
\[\Rightarrow BM=\dfrac{a}{2}=\dfrac{24}{2}=12cm\], where ‘a’ is the side of the equilateral triangle.
Therefore, applying \[\tan \theta \] = (perpendicular / base), where \[\theta ={{30}^{\circ }}\], we get,
\[\begin{align}
  & \Rightarrow \tan {{30}^{\circ }}=\dfrac{OM}{BM}=\dfrac{r}{\left( \dfrac{a}{2} \right)} \\
 & \Rightarrow \tan {{30}^{\circ }}=\dfrac{2r}{a} \\
\end{align}\]
Substituting, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\] and a = 24, we get,
\[\begin{align}
  & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{2r}{24} \\
 & \Rightarrow r=\dfrac{12}{\sqrt{3}}cm \\
\end{align}\]
Therefore, area of the remaining portion of the triangle = area of the shaded part
Area = Area (\[\Delta ABC\]) – Area of the circle
We know that, area of equilateral triangle = \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\] and area of circle = \[\pi {{r}^{2}}\], therefore, we have,
\[\Rightarrow \] Area of the remaining portion = \[\dfrac{\sqrt{3}}{4}\times {{\left( 24 \right)}^{2}}-\pi \times {{\left( \dfrac{12}{\sqrt{3}} \right)}^{2}}\]
\[\Rightarrow \] Area of the remaining portion = \[\dfrac{\sqrt{3}}{4}\times {{\left( 12 \right)}^{2}}\times 4-\dfrac{\pi \times {{\left( 12 \right)}^{2}}}{3}\]
\[\Rightarrow \] Area of the remaining portion = \[{{\left( 12 \right)}^{2}}\times \left[ \sqrt{3}-\dfrac{\pi }{3} \right]\]
Substituting \[\sqrt{3}=1.732\] and \[\pi =\dfrac{22}{7}\], we get,
\[\Rightarrow \] Area of the remaining portion = \[144\times \left[ 1.732-\dfrac{22}{3\times 7} \right]\]
\[\Rightarrow \] Area of the remaining portion = \[144\times \left[ 1.732-1.047 \right]\]
\[\Rightarrow \] Area of the remaining portion = \[98.55c{{m}^{2}}\]

So, the correct answer is “Option b”.

Note: One may note that we have substituted the value of \[\pi \] equal to \[\dfrac{22}{7}\] because no information was provided regarding \[\pi \] in the question. One can also substitute \[\pi =3.14\] as it will not change the answer but only the digits after the decimal will change. Remember that here we do not have to take the sum of the areas of the triangle and circle because we have been asked to find the area of the remaining portion. So, we must consider the differences between the areas.