Question

In an equilateral triangle, (circumradius) : (inradius) : (exradius) is equal to,
A. 1:1:1
B. 1:2:3
C. 2:1:3
D. 3:2:4

Answer 1

Hint: We use some trigonometric formulas for finding the value of circumradius, inradius and exradius, in terms of the side of the triangle. We draw the diagram of incircle,circumcircle and excircle to show the relationship between radius and sides.

Complete step-by-step answer:
Let us assume the length of the sides of the equilateral triangle to be a, and the triangle to be \[\Delta ABC\].
First, let us find the circumradius.

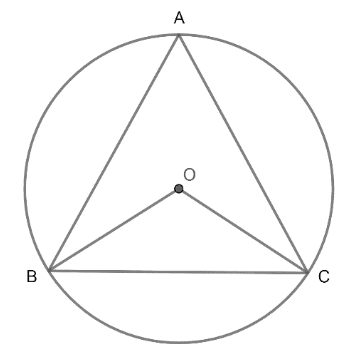
O is the centre of the circumcircle of the triangle.
We know that the angle made by a segment at the centre is twice the angle made by it on the circumference.
$\therefore \angle BOC=2\angle BAC$
$\angle BAC=60{}^\circ $ since \[\Delta ABC\] is an equilateral $\Delta $.
$\Rightarrow \angle BOC=120{}^\circ $
Let us apply the cosine formula on $\angle BOC$ in $\Delta BOC$.
OB and OC are the radii of the circumcircle of \[\Delta ABC\]. Let us assume them to be R.
According to cosine formula,
$\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
We apply the above formula here,
$\begin{align}
  & \cos \angle BOC=\dfrac{O{{B}^{2}}+O{{C}^{2}}-B{{C}^{2}}}{\left( O.B \right)\left( OC \right)} \\
 & \cos 120{}^\circ =\dfrac{{{R}^{2}}+{{R}^{2}}-{{a}^{2}}}{2{{R}^{2}}} \\
\end{align}$
$\begin{align}
  & -\dfrac{1}{2}=\dfrac{{{R}^{2}}+{{R}^{2}}-{{a}^{2}}}{2{{R}^{2}}} \\
 & -{{R}^{2}}={{R}^{2}}+{{R}^{2}}-{{a}^{2}} \\
 & 3{{R}^{2}}={{a}^{2}} \\
 & \Rightarrow R=\dfrac{a}{\sqrt{3}}. \\
 & \therefore \ \text{circumradius}=\dfrac{a}{\sqrt{3}}. \\
\end{align}$
Now, let us find the inradius.

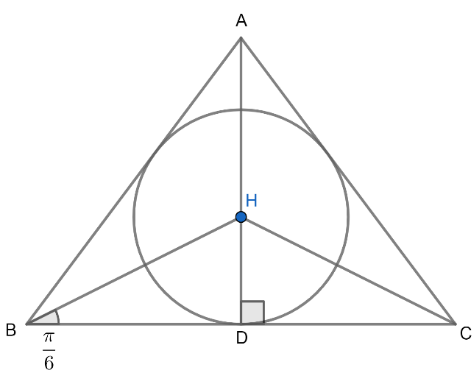
AD is perpendicular to BC.
HD is the inradius of $\Delta ABC$.
In an equilateral $\Delta $, perpendicular divides the base in two equal parts.
$\therefore BD=CD=\dfrac{a}{2}$
Let us assume HD to be r.
In $\Delta BHD$,
$\begin{align}
  & \tan \left( \angle HBD \right)=\dfrac{HD}{BD} \\
 & \tan \left( 30{}^\circ \right)=\dfrac{r}{\dfrac{a}{2}} \\
 & \dfrac{1}{\sqrt{3}}=\dfrac{2r}{a} \\
 & \Rightarrow r=\dfrac{a}{2\sqrt{3}}. \\
 & \therefore inradius=\dfrac{a}{2\sqrt{3}}. \\
\end{align}$
Now, we find the excircle of the triangle:

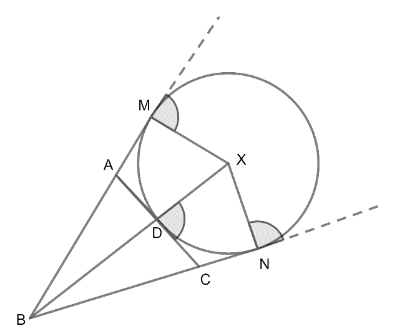
X is the centre of the excircle of $\Delta ABC$.
BD is the perpendicular from B to D joining X.
In equilateral, altitude is the angle bisector of the triangle.
$\begin{align}
  & \therefore \angle ABX=\dfrac{1}{2}\angle ABC=30{}^\circ \\
 & \dfrac{BD}{AD}=\tan \dfrac{\pi }{3} \\
 & \Rightarrow BD=\dfrac{\sqrt{3}}{2}a \\
\end{align}$
$\begin{align}
  & MX=DX=x=exradius\ of\ \Delta ABC. \\
 & In\ \Delta MBX, \\
 & \sin \left( \angle MBX \right)=\dfrac{MX}{BX} \\
 & \sin \left( \dfrac{\pi }{6} \right)=\dfrac{MX}{BD+DX} \\
 & \dfrac{1}{2}=\dfrac{x}{x+\dfrac{\sqrt{3}}{2}a} \\
 & \Rightarrow x+\dfrac{\sqrt{3}}{2}a=2x \\
 & \Rightarrow x=\dfrac{\sqrt{3}}{2}a \\
\end{align}$
Hence, exradius is $\dfrac{\sqrt{3}}{2}a$.
Circumradius : inradius : exradius
$\begin{align}
  & \Rightarrow R:r:x \\
 & =\dfrac{a}{\sqrt{3}}:\dfrac{a}{2\sqrt{3}}:\dfrac{\sqrt{3}}{2}a \\
 & =2:1:3 \\
\end{align}$
Therefore the answer is 2:1:3.

Note: We can directly use the formula for a general $\Delta $.
Inradius $=\sqrt{\dfrac{\left( s-a \right)\left( s-b \right)\left( s-c \right)}{s}}$
Circumradius $=\dfrac{abc}{4\Delta }$
Exradius: ${{r}_{1}}=\dfrac{\Delta }{s-a}$
where $\Delta $ is the area of the $\Delta $.