
In an equilateral triangle \[ABC\], the side \[BC\] is trisected at \[D\]. Prove that \[9A{D^2} = 7A{B^2}\].
Answer
585.9k+ views
Hint:
We are given an equilateral triangle where one side is trisected. We are required to prove \[9A{D^2} = 7A{B^2}\]. To do that, we will drop a bisector on the side which is trisected. Then we will apply the Pythagoras theorem to the right-angled triangle formed by the bisector and the trisector to obtain the result.
Formula Used: Here, we will use the formula of Pythagoras theorem, \[{\rm\text{Hypotenus}}{{\rm{e}}^2} = {\rm\text{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\].
Complete step by step solution:
We are given an equilateral triangle \[ABC\]. The side \[BC\] is trisected at \[D\]. Let the side of the triangle be \[a\].
To solve this question, we will need to do one construction.
Construction- Drop a perpendicular from A on \[BC\], say at a point E. We know that the perpendicular is also the bisector for the side \[BC\], as this is an equilateral triangle.
Based on the above information, we will draw a diagram for a better understanding.
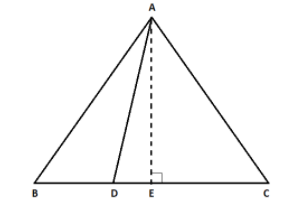
In \[\Delta ABE\],
\[{\rm{Hypotenuse}} = AB = a\] [side of the triangle]
\[{\rm{Base}} = BE = \dfrac{a}{2}\] [\[BC\] is perpendicularly bisected at point E, hence, \[BC = 2BE\]or \[2BE = a\]]
\[{\rm{Perpendicular}} = AE\]
We will apply the Pythagoras theorem to \[\Delta ABE\], to find the value of \[AE\]. Now we will substitute the above values in the formula \[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\].
\[\begin{array}{l}{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\\ \Rightarrow A{B^2} = A{E^2} + B{E^2}\end{array}\]
Substituting \[AB = a\] and \[BE = \dfrac{a}{2}\] in the above equation, we get
\[\begin{array}{l} \Rightarrow {a^2} = A{E^2} + {\left[ {\dfrac{a}{2}} \right]^2}\\ \Rightarrow A{E^2} = {a^2} - \dfrac{{{a^2}}}{4}\end{array}\]
Subtracting the like terms, we get
\[A{E^2} = \dfrac{{3{a^2}}}{4}\]
Taking square root on both sides, we get
\[\begin{array}{c}AE = \sqrt {\dfrac{{3{a^2}}}{4}} \\ = \dfrac{{a\sqrt 3 }}{2}\end{array}\]
Now, we know that
\[BE = \dfrac{a}{2}\] ( \[BC\] is perpendicularly bisected at point E, hence, \[BC = 2BE\]or \[2BE = a\] ).
\[BD = \dfrac{a}{3}\] ( \[BD\] is trisected at point D, hence, \[BC = 3BD\]or \[3BD = a\] ).
Thus, \[DE = BE - BD\]
\[\begin{array}{c}DE = \dfrac{a}{2} - \dfrac{a}{3}\\ = \dfrac{{3a}}{6} - \dfrac{{2a}}{6}\\ = \dfrac{a}{6}\end{array}\]
As we have found \[AE\] and \[DE\] now, let us apply the Pythagoras theorem to \[\Delta ADE\].
In \[\Delta ADE\],
\[{\rm{Hypotenuse}} = AD\]
\[{\rm{Base}} = DE = \dfrac{a}{6}\]
\[{\rm{Perpendicular}} = AE = \dfrac{{a\sqrt 3 }}{2}\]
On applying the Pythagoras theorem to \[\Delta ADE\], to find the value of \[AD\].
Substitute the above values in the formula to obtain the value of \[AD\].
\[\begin{array}{l}{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\\ \Rightarrow A{D^2} = A{E^2} + B{D^2}\\ \Rightarrow A{D^2} = {\left[ {\dfrac{{a\sqrt 3 }}{2}} \right]^2} + {\left[ {\dfrac{a}{6}} \right]^2}\end{array}\]
On taking the LCM,
\[\begin{array}{l} \Rightarrow A{D^2} = \dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{{36}}\\ \Rightarrow A{D^2} = \dfrac{{9\left[ {3{a^2}} \right]}}{{36}} + \dfrac{{{a^2}}}{{36}}\end{array}\]
Now we will multiply the terms and then add them.
\[\begin{array}{l} \Rightarrow A{D^2} = \dfrac{{27{a^2}}}{{36}} + \dfrac{{{a^2}}}{{36}}\\ \Rightarrow A{D^2} = \dfrac{{28{a^2}}}{{36}}\end{array}\]
We will simplify our answer further by dividing the numerator and denominator with 4.
\[ \Rightarrow A{D^2} = \dfrac{{7{a^2}}}{9}\]…………..\[\left[ i \right]\]
Now, we know that \[a\] is the side of the triangle. Hence, we can replace \[a\] with\[AB\] in equation \[\left[ i \right]\]. On doing so, equation \[\left[ i \right]\] becomes –
\[\begin{array}{l}A{D^2} = \dfrac{{7A{B^2}}}{9}\\ \Rightarrow 9A{D^2} = 7A{B^2}\end{array}\]
Hence, we have proved that \[9A{D^2} = 7A{B^2}\].
Note:
The alternate method to solve this question can be as follows –
We are given an equilateral triangle \[ABC\]. The side \[BC\] is trisected at \[D\].
To solve this question, we will need to do one construction.
Construction- Drop a perpendicular from A on \[BC\], say at a point E. We know that the perpendicular is also the bisector for the side \[BC\], as this is an equilateral triangle.
Based on the above information, draw a diagram for a better understanding.
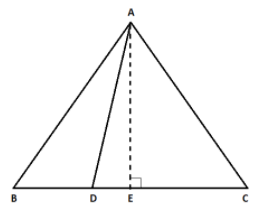
On applying the Pythagoras theorem to the right-angled \[\Delta ADE\], we get –
\[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\]
\[A{D^2} = A{E^2} + D{E^2}\]……………..\[\left[ 1 \right]\]
On applying the Pythagoras theorem to the right-angled \[\Delta ABE\], we get –
\[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\]
\[A{B^2} = A{E^2} + B{E^2}\]………….….\[\left[ 2 \right]\]
Now subtracting equation \[\left[ 1 \right]\] from equation \[\left[ 2 \right]\], we get,
\[\begin{array}{c}A{D^2} - A{B^2} = A{E^2} + D{E^2} - \left[ {A{E^2} + B{E^2}} \right]\\ = A{E^2} + D{E^2} - A{E^2} - B{E^2}\end{array}\]
\[A{D^2} - A{B^2} = D{E^2} - B{E^2}\]………….\[\left[ 3 \right]\]
Now we will substitute \[DE\]with \[BE - BD\] in equation \[\left[ 3 \right]\].
\[A{D^2} - A{B^2} = {\left[ {BE - BD} \right]^2} - B{E^2}\]………….\[\left[ 4 \right]\]
Now we know that,
\[BE = \dfrac{{BC}}{2}\]……….\[\left[ 5 \right]\] [Since \[AE\] is the perpendicular bisector]
\[BD = \dfrac{{BC}}{3}\] …………\[\left[ 6 \right]\] [Since \[AD\] is the trisector]
On substituting the values of \[BE\] and \[BD\] from equation \[\left[ 5 \right]\] and equation \[\left[ 6 \right]\] respectively to equation \[\left[ 4 \right]\], we get,
\[\begin{array}{l}A{D^2} - A{B^2} = {\left[ {BE - BD} \right]^2} - B{E^2}\\ \Rightarrow A{D^2} - A{B^2} = {\left[ {\dfrac{{BC}}{2} - \dfrac{{BC}}{3}} \right]^2} - {\left[ {\dfrac{{BC}}{2}} \right]^2}\end{array}\]
Simplifying the equation, we get
\[\begin{array}{l} \Rightarrow A{D^2} - A{B^2} = {\left[ {\dfrac{{3BC}}{6} - \dfrac{{2BC}}{6}} \right]^2} - \dfrac{{B{C^2}}}{4}\\ \Rightarrow A{D^2} - A{B^2} = {\left[ {\dfrac{{BC}}{6}} \right]^2} - \dfrac{{B{C^2}}}{4}\end{array}\]
Apply the exponent on the terms, we get
\[ \Rightarrow A{D^2} - A{B^2} = {\dfrac{{BC}}{{36}}^2} - \dfrac{{B{C^2}}}{4}\]………..\[\left[ 7 \right]\]
Now, since our triangle is equilateral so \[AB = BC\]. Substitute \[BC\] with \[AB\] in equation \[\left[ 7 \right]\], we will obtain,
\[\begin{array}{l}A{D^2} - A{B^2} = {\dfrac{{BC}}{{36}}^2} - \dfrac{{B{C^2}}}{4}\\ \Rightarrow A{D^2} - A{B^2} = {\dfrac{{AB}}{{36}}^2} - \dfrac{{A{B^2}}}{4}\end{array}\]
Adding on both the sides, we get
\[\begin{array}{l} \Rightarrow A{D^2} = A{B^2} + {\dfrac{{AB}}{{36}}^2} - \dfrac{{A{B^2}}}{4}\\ \Rightarrow A{D^2} = \dfrac{{36A{B^2}}}{{36}} + {\dfrac{{AB}}{{36}}^2} - \dfrac{{9A{B^2}}}{{36}}\end{array}\]
Simplifying the above equation, we get
\[\begin{array}{l} \Rightarrow A{D^2} = \dfrac{{28A{B^2}}}{{36}}\\ \Rightarrow A{D^2} = \dfrac{{7A{B^2}}}{9}\end{array}\]
On cross multiplication, we get
\[ \Rightarrow 9A{D^2} = 7A{B^2}\]
Hence, we proved that \[9A{D^2} = 7A{B^2}\].
We are given an equilateral triangle where one side is trisected. We are required to prove \[9A{D^2} = 7A{B^2}\]. To do that, we will drop a bisector on the side which is trisected. Then we will apply the Pythagoras theorem to the right-angled triangle formed by the bisector and the trisector to obtain the result.
Formula Used: Here, we will use the formula of Pythagoras theorem, \[{\rm\text{Hypotenus}}{{\rm{e}}^2} = {\rm\text{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\].
Complete step by step solution:
We are given an equilateral triangle \[ABC\]. The side \[BC\] is trisected at \[D\]. Let the side of the triangle be \[a\].
To solve this question, we will need to do one construction.
Construction- Drop a perpendicular from A on \[BC\], say at a point E. We know that the perpendicular is also the bisector for the side \[BC\], as this is an equilateral triangle.
Based on the above information, we will draw a diagram for a better understanding.

In \[\Delta ABE\],
\[{\rm{Hypotenuse}} = AB = a\] [side of the triangle]
\[{\rm{Base}} = BE = \dfrac{a}{2}\] [\[BC\] is perpendicularly bisected at point E, hence, \[BC = 2BE\]or \[2BE = a\]]
\[{\rm{Perpendicular}} = AE\]
We will apply the Pythagoras theorem to \[\Delta ABE\], to find the value of \[AE\]. Now we will substitute the above values in the formula \[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\].
\[\begin{array}{l}{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\\ \Rightarrow A{B^2} = A{E^2} + B{E^2}\end{array}\]
Substituting \[AB = a\] and \[BE = \dfrac{a}{2}\] in the above equation, we get
\[\begin{array}{l} \Rightarrow {a^2} = A{E^2} + {\left[ {\dfrac{a}{2}} \right]^2}\\ \Rightarrow A{E^2} = {a^2} - \dfrac{{{a^2}}}{4}\end{array}\]
Subtracting the like terms, we get
\[A{E^2} = \dfrac{{3{a^2}}}{4}\]
Taking square root on both sides, we get
\[\begin{array}{c}AE = \sqrt {\dfrac{{3{a^2}}}{4}} \\ = \dfrac{{a\sqrt 3 }}{2}\end{array}\]
Now, we know that
\[BE = \dfrac{a}{2}\] ( \[BC\] is perpendicularly bisected at point E, hence, \[BC = 2BE\]or \[2BE = a\] ).
\[BD = \dfrac{a}{3}\] ( \[BD\] is trisected at point D, hence, \[BC = 3BD\]or \[3BD = a\] ).
Thus, \[DE = BE - BD\]
\[\begin{array}{c}DE = \dfrac{a}{2} - \dfrac{a}{3}\\ = \dfrac{{3a}}{6} - \dfrac{{2a}}{6}\\ = \dfrac{a}{6}\end{array}\]
As we have found \[AE\] and \[DE\] now, let us apply the Pythagoras theorem to \[\Delta ADE\].
In \[\Delta ADE\],
\[{\rm{Hypotenuse}} = AD\]
\[{\rm{Base}} = DE = \dfrac{a}{6}\]
\[{\rm{Perpendicular}} = AE = \dfrac{{a\sqrt 3 }}{2}\]
On applying the Pythagoras theorem to \[\Delta ADE\], to find the value of \[AD\].
Substitute the above values in the formula to obtain the value of \[AD\].
\[\begin{array}{l}{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\\ \Rightarrow A{D^2} = A{E^2} + B{D^2}\\ \Rightarrow A{D^2} = {\left[ {\dfrac{{a\sqrt 3 }}{2}} \right]^2} + {\left[ {\dfrac{a}{6}} \right]^2}\end{array}\]
On taking the LCM,
\[\begin{array}{l} \Rightarrow A{D^2} = \dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{{36}}\\ \Rightarrow A{D^2} = \dfrac{{9\left[ {3{a^2}} \right]}}{{36}} + \dfrac{{{a^2}}}{{36}}\end{array}\]
Now we will multiply the terms and then add them.
\[\begin{array}{l} \Rightarrow A{D^2} = \dfrac{{27{a^2}}}{{36}} + \dfrac{{{a^2}}}{{36}}\\ \Rightarrow A{D^2} = \dfrac{{28{a^2}}}{{36}}\end{array}\]
We will simplify our answer further by dividing the numerator and denominator with 4.
\[ \Rightarrow A{D^2} = \dfrac{{7{a^2}}}{9}\]…………..\[\left[ i \right]\]
Now, we know that \[a\] is the side of the triangle. Hence, we can replace \[a\] with\[AB\] in equation \[\left[ i \right]\]. On doing so, equation \[\left[ i \right]\] becomes –
\[\begin{array}{l}A{D^2} = \dfrac{{7A{B^2}}}{9}\\ \Rightarrow 9A{D^2} = 7A{B^2}\end{array}\]
Hence, we have proved that \[9A{D^2} = 7A{B^2}\].
Note:
The alternate method to solve this question can be as follows –
We are given an equilateral triangle \[ABC\]. The side \[BC\] is trisected at \[D\].
To solve this question, we will need to do one construction.
Construction- Drop a perpendicular from A on \[BC\], say at a point E. We know that the perpendicular is also the bisector for the side \[BC\], as this is an equilateral triangle.
Based on the above information, draw a diagram for a better understanding.

On applying the Pythagoras theorem to the right-angled \[\Delta ADE\], we get –
\[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\]
\[A{D^2} = A{E^2} + D{E^2}\]……………..\[\left[ 1 \right]\]
On applying the Pythagoras theorem to the right-angled \[\Delta ABE\], we get –
\[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\]
\[A{B^2} = A{E^2} + B{E^2}\]………….….\[\left[ 2 \right]\]
Now subtracting equation \[\left[ 1 \right]\] from equation \[\left[ 2 \right]\], we get,
\[\begin{array}{c}A{D^2} - A{B^2} = A{E^2} + D{E^2} - \left[ {A{E^2} + B{E^2}} \right]\\ = A{E^2} + D{E^2} - A{E^2} - B{E^2}\end{array}\]
\[A{D^2} - A{B^2} = D{E^2} - B{E^2}\]………….\[\left[ 3 \right]\]
Now we will substitute \[DE\]with \[BE - BD\] in equation \[\left[ 3 \right]\].
\[A{D^2} - A{B^2} = {\left[ {BE - BD} \right]^2} - B{E^2}\]………….\[\left[ 4 \right]\]
Now we know that,
\[BE = \dfrac{{BC}}{2}\]……….\[\left[ 5 \right]\] [Since \[AE\] is the perpendicular bisector]
\[BD = \dfrac{{BC}}{3}\] …………\[\left[ 6 \right]\] [Since \[AD\] is the trisector]
On substituting the values of \[BE\] and \[BD\] from equation \[\left[ 5 \right]\] and equation \[\left[ 6 \right]\] respectively to equation \[\left[ 4 \right]\], we get,
\[\begin{array}{l}A{D^2} - A{B^2} = {\left[ {BE - BD} \right]^2} - B{E^2}\\ \Rightarrow A{D^2} - A{B^2} = {\left[ {\dfrac{{BC}}{2} - \dfrac{{BC}}{3}} \right]^2} - {\left[ {\dfrac{{BC}}{2}} \right]^2}\end{array}\]
Simplifying the equation, we get
\[\begin{array}{l} \Rightarrow A{D^2} - A{B^2} = {\left[ {\dfrac{{3BC}}{6} - \dfrac{{2BC}}{6}} \right]^2} - \dfrac{{B{C^2}}}{4}\\ \Rightarrow A{D^2} - A{B^2} = {\left[ {\dfrac{{BC}}{6}} \right]^2} - \dfrac{{B{C^2}}}{4}\end{array}\]
Apply the exponent on the terms, we get
\[ \Rightarrow A{D^2} - A{B^2} = {\dfrac{{BC}}{{36}}^2} - \dfrac{{B{C^2}}}{4}\]………..\[\left[ 7 \right]\]
Now, since our triangle is equilateral so \[AB = BC\]. Substitute \[BC\] with \[AB\] in equation \[\left[ 7 \right]\], we will obtain,
\[\begin{array}{l}A{D^2} - A{B^2} = {\dfrac{{BC}}{{36}}^2} - \dfrac{{B{C^2}}}{4}\\ \Rightarrow A{D^2} - A{B^2} = {\dfrac{{AB}}{{36}}^2} - \dfrac{{A{B^2}}}{4}\end{array}\]
Adding on both the sides, we get
\[\begin{array}{l} \Rightarrow A{D^2} = A{B^2} + {\dfrac{{AB}}{{36}}^2} - \dfrac{{A{B^2}}}{4}\\ \Rightarrow A{D^2} = \dfrac{{36A{B^2}}}{{36}} + {\dfrac{{AB}}{{36}}^2} - \dfrac{{9A{B^2}}}{{36}}\end{array}\]
Simplifying the above equation, we get
\[\begin{array}{l} \Rightarrow A{D^2} = \dfrac{{28A{B^2}}}{{36}}\\ \Rightarrow A{D^2} = \dfrac{{7A{B^2}}}{9}\end{array}\]
On cross multiplication, we get
\[ \Rightarrow 9A{D^2} = 7A{B^2}\]
Hence, we proved that \[9A{D^2} = 7A{B^2}\].
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





