Question

In an equilateral triangle ABC, the side BC is trisected at point D. Prove that \[9A{D^2} = 7A{B^2}\].

Answer 1

Hint:
Here, we need to prove that \[9A{D^2} = 7A{B^2}\]. We will join A to point M on the line segment BC, such that AM is perpendicular to BC. We will use congruence of triangles, Pythagoras’s theorem, and the properties of line segments to prove the required expression. If a point Y lies on the line segment XZ, then the length of XZ is the sum of the lengths XY and YZ.

Complete step by step solution:
First, we will join A to point M on the line segment BC, such that AM is perpendicular to BC.
Thus, we get the diagram

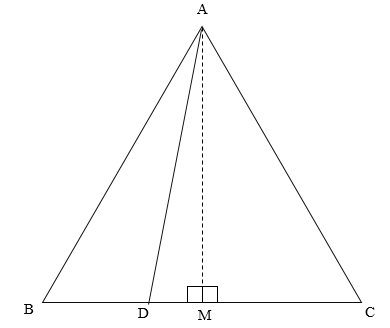
It is given that triangle ABC is an equilateral triangle.
Therefore, we get
\[AB = BC = AC\]
Since AM is perpendicular to BC, \[\angle AMC\], \[\angle AMD\], and \[\angle AMB\] are of measure 90 degrees.
Therefore, triangles AMB, AMC, and AMD are right angled triangles.
Now, in triangles AMB and AMC, we have
\[AB = AC\] (sides of an equilateral triangle are equal)
\[\angle AMB = \angle AMC = 90^\circ \] (since AM is perpendicular to BC)
\[AM = AM\] (common side)
Therefore, by R.H.S. congruence criterion, the triangles AMB and AMC are congruent.
We know that corresponding parts of congruent triangles are equal.
Thus, we get
\[BM = CM\]
We can observe that the line segment BC is the sum of the line segments BM and MC.
Therefore, we get
\[ \Rightarrow BM + MC = BC\]
Substituting \[BM = CM\] in the equation, we get
\[ \Rightarrow BM + BM = BC\]
Adding the like terms, we get
\[ \Rightarrow 2BM = BC\]
Dividing both sides of the equation by 2, we get
\[ \Rightarrow BM = \dfrac{1}{2}BC\]
Thus, we get
\[ \Rightarrow BM = MC = \dfrac{1}{2}BC\]
Now, it is given that the point D trisects the line segment BC.
Therefore, the line segments BD and DC are in the ratio 1: 2.
Thus, we get
\[\dfrac{{BD}}{{DC}} = \dfrac{1}{2}\]
Multiplying both sides of the equation by 2, we get
\[ \Rightarrow 2BD = DC\]
We can observe that the line segment BC is the sum of the line segments BD and DC.
Therefore, we get
\[ \Rightarrow BD + DC = BC\]
Substituting \[DC = 2BD\] in the equation, we get
\[ \Rightarrow BD + 2BD = BC\]
Adding the like terms, we get
\[ \Rightarrow 3BD = BC\]
Dividing both sides of the equation by 3, we get
\[ \Rightarrow BD = \dfrac{1}{3}BC\]
Next, we can observe that the line segment DM is the difference of the lengths of the line segments BM and BD.
Therefore, we get
\[ \Rightarrow DM = BM - BD\]
Substituting \[BM = \dfrac{1}{2}BC\] and \[BD = \dfrac{1}{3}BC\] in the equation, we get
\[ \Rightarrow DM = \dfrac{1}{2}BC - \dfrac{1}{3}BC\]
Subtracting the like terms by taking L.C.M., we get
\[\begin{array}{l} \Rightarrow DM = \dfrac{{3 - 2}}{6}BC\\ \Rightarrow DM = \dfrac{1}{6}BC\end{array}\]
Now, we will use Pythagoras's theorem in the right angled triangle AMD.
In triangle AMD, AD is the hypotenuse, DM is the base, and AM is the height.
Therefore, in triangle AMD, we get
\[ \Rightarrow A{D^2} = D{M^2} + A{M^2}\]……………………………….\[\left( 1 \right)\]
In the right angled triangle AMC, AC is the hypotenuse, CM is the base, and AM is the height.
Applying the Pythagoras’s theorem in triangle AMC, we get
\[ \Rightarrow A{C^2} = C{M^2} + A{M^2}\]………………………………….\[\left( 2 \right)\]
Subtracting both sides of equation \[\left( 2 \right)\] from equation \[\left( 1 \right)\], we get
\[ \Rightarrow A{D^2} - A{C^2} = D{M^2} + A{M^2} - C{M^2} - A{M^2}\]
Subtracting the like terms, we get
\[ \Rightarrow A{D^2} - A{C^2} = D{M^2} - C{M^2}\]
Substituting \[DM = \dfrac{1}{6}BC\] and \[CM = \dfrac{1}{2}BC\] in the equation, we get
\[ \Rightarrow A{D^2} - A{C^2} = {\left( {\dfrac{1}{6}BC} \right)^2} - {\left( {\dfrac{1}{2}BC} \right)^2}\]
Applying the exponents on the bases, we get
\[ \Rightarrow A{D^2} - A{C^2} = \dfrac{1}{{36}}B{C^2} - \dfrac{1}{4}B{C^2}\]
Adding \[A{C^2}\] on both sides of the equation, we get
\[ \Rightarrow A{D^2} = \dfrac{1}{{36}}B{C^2} - \dfrac{1}{4}B{C^2} + A{C^2}\]
Substituting \[BC = AB\] and \[AC = AB\] in the equation, we get
\[ \Rightarrow A{D^2} = \dfrac{1}{{36}}A{B^2} - \dfrac{1}{4}A{B^2} + A{B^2}\]
Subtracting the terms by taking the L.C.M., we get
\[ \Rightarrow A{D^2} = \dfrac{{1 - 9 + 36}}{{36}}A{B^2}\]
Simplifying the expression, we get
\[ \Rightarrow A{D^2} = \dfrac{{28}}{{36}}A{B^2}\]
Simplifying the fraction, we get
\[ \Rightarrow A{D^2} = \dfrac{7}{9}A{B^2}\]
Finally, multiplying both sides of the equation by 9, we get
\[ \Rightarrow 9A{D^2} = 7A{B^2}\]

\[\therefore \] We have proved that \[9A{D^2} = 7A{B^2}\].

Note:
We used Pythagoras's theorem in the triangles AMD and AMC. The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}\]. The hypotenuse of a right angled triangle is its longest side.
We proved that the triangle AMB and AMC are congruent by the R.H.S. congruence criterion. According to the R.H.S. congruence criterion, if two triangles are right angled triangles such that their corresponding hypotenuse, and one pair of corresponding sides are equal, then the two triangles are congruent.