Question

In an AC circuit, the current lags behind the voltage by \[{\pi }/{3}\;\]. The components of the circuit are:
A. R and L
B. L and C
C. R and C
D. Only R

Answer 1

Hint: In a series L-R circuit, the current lags behind the voltage by a constant angle.

Complete step by step solution:
In a series L-R circuit, let an alternating emf \[E={{E}_{\text{o}}}\sin \omega t\] be applied to it.
Let i be the current in the circuit at any instant and \[{{V}_{L}}\] and \[{{V}_{R}}\] be the voltage across L and R respectively at that instant.
Then \[{{V}_{L}}=i{{X}_{L}}\] and \[{{V}_{R}}=iR\], where \[{{X}_{L}}\] is the inductive reactance. Now, \[{{V}_{R}}\] is in phase with the current i, while \[{{V}_{L}}\] leads i by \[{{90}^{\text{o}}}\].

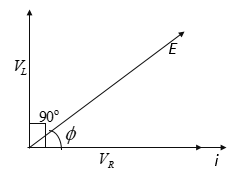
The phasor diagram above shows that , in L-R circuit, the voltage leads the current by a phase angle \[\phi \] is given by:
\[\begin{align}
  & \tan \phi =\dfrac{{{V}_{L}}}{{{V}_{R}}}=\dfrac{i{{X}_{L}}}{iR}=\dfrac{\omega L}{R} \\
 & \text{ }\phi ={{\tan }^{-1}}\dfrac{\omega L}{R} \\
\end{align}\]
So, if in an AC circuit, the current lags behind the voltage by \[{\pi }/{3}\;\]. The components of the circuit are L and R.
Therefore option A. is the correct answer.

Additional information:
In a pure resistor circuit, the current is always in phase with the voltage.
In a C-R circuit, the voltage lags behind the current by a constant angle.
In a L-C circuit, the voltage across L leads the current in phase by \[{{90}^{\text{o}}}\], while the voltage across C lags behind the current in phase by \[{{90}^{\text{o}}}\]. The phase difference between \[{{V}_{L}}\] and \[{{V}_{C}}\] is \[{{180}^{\text{o}}}\].

Note: The inductor and resistance in a L-R circuit is connected in series. In the L-R circuit , \[{{V}_{L}}\] and \[{{V}_{R}}\] are mutually at right angles. Their sum is not equal to the impressed emf E.
Form the equation of phase angle, it is clear that if \[L=0\], then \[\phi =0\](the emf and the current will be in the same phase); if \[R=0\] then \[\phi ={{90}^{\text{o}}}\](the emf will lead the current by \[{{90}^{\text{o}}}\]).