Question

In △ABC, with radius of circumcircle as 2 and radius of incircle as \[\sqrt{3}-1\] , let AD,BE and CF be perpendicular from A,B and C upon the opposite sides of the triangle intersecting each other at O, then Arithmetic mean of OA,OB and OC is
A. \[\dfrac{2}{3}(\sqrt{3}+1)\]
B. \[\dfrac{2}{3}\left( \sqrt{3}-1 \right)\]
C. \[\dfrac{\sqrt{3}+1}{3}\]
D. \[\dfrac{\sqrt{3}-1}{3}\]

Answer 1

Hint: By drawing and pointing the triangle and drawing the perpendiculars on three sides and writing the arithmetic mean we are almost to the solution, by simplifying all the trigonometric properties we get the solution.

Complete step-by-step answer:
Given △ABC with radius of circumcircle as 2 and radius of incircle as \[\sqrt{3}-1\].

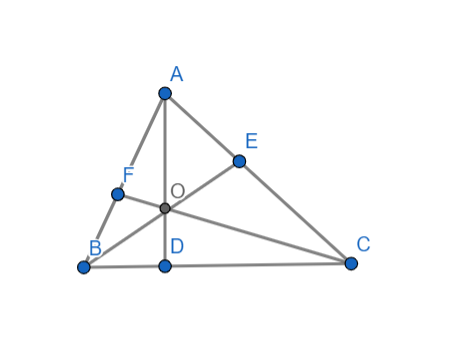
Given △ABC with radius of circumcircle as 2 and radius of incircle as \[\sqrt{3}-1\].
\[\begin{align}
  & OA=2R\cos A \\
 & OB=2R\cos B \\
 & OC=2R\cos C \\
\end{align}\]
Arithmetic mean of of OA,OB and OC,
\[=\dfrac{2R}{3}\left( \cos A+\cos B+\cos C \right)\]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (a)
\[\left( \cos A+\cos B+\cos C \right)\]= \[\left( 1+4\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2} \right)\] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
We have to substitute the value of equation (1) in (a),
\[=\dfrac{2R}{3}\left( 1+4\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2} \right)\]
Since r= \[\left( 1+4R\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2} \right)\]
We get \[=\dfrac{2R}{3}\left( 1+r \right)\]
\[=\dfrac{2R}{3}+\dfrac{2r}{3}\]
By substituting the values of R and r in the above equation we get
\[=\dfrac{2}{3}\left( 2+\sqrt{3}-1 \right)\]
\[=\dfrac{2}{3}\left( \sqrt{3}+1 \right)\]
Therefore the option is A.

Note: Drawing of the figure plays a key role in this type of problem. Finding the arithmetic mean of all the perpendicular drawn from o. As there are many trigonometric properties care should be taken while solving.