
In a \[\vartriangle ABC\], if \[{a^2} + {b^2} + {c^2} = ac + \sqrt 3 ab\], then the triangle is
A. Equilateral
B. right angled and isosceles
C. right angled and not isosceles
D. None of the above
Answer
569.1k+ views
Hint: We use sine rule to write the value of each side in terms of its opposite angle. Substitute the values of sides in the equation and cancel common terms. Take \[2\sin A\] common from terms in RHS such that the bracket inside forms an identity of trigonometry.
* Law of sine states that in a triangle ABC the ratio of side of a triangle to the sine of opposite angle is same for all the sides of the triangle, i.e. if side a has opposite angle A, side b has opposite angle B and side c has opposite angle C, then we can write \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\] where k is some constant term.
* Isosceles triangle has two sides of equal length and the angles opposite to equal sides are equal in measure.
* Equilateral triangle has all its sides of equal length and all its angles of equal measure.
* Right angled triangle has one of its angles as a right angle i.e. \[{90^ \circ }\]
Complete step-by-step solution:
Given equation is \[{a^2} + {b^2} + {c^2} = ac + \sqrt 3 ab\]..................… (1)
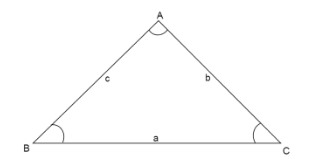
We have a triangle ABC, where side A has opposite angle A, side B has opposite angle B and side c has opposite angle C. So we can apply sine rule in the triangle.
i.e. \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\]
On cross multiplication of terms we get
\[a = k\sin A;b = k\sin B;c = k\sin C\]
Substitute the values of ‘a’, ‘b’ and ‘c’ in equation (1)
\[ \Rightarrow {\left( {k\sin A} \right)^2} + {\left( {k\sin B} \right)^2} + {\left( {k\sin C} \right)^2} = \left( {k\sin A} \right)\left( {k\sin C} \right) + \sqrt 3 \left( {k\sin A} \right)\left( {k\sin B} \right)\]
Write the multiplication of terms on both sides of the equation
\[ \Rightarrow {k^2}{\sin ^2}A + {k^2}{\sin ^2}B + {k^2}{\sin ^2}C = {k^2}\sin A\sin C + \sqrt 3 {k^2}\sin A\sin B\]
Take constant term common on both sides of the equation
\[ \Rightarrow {k^2}\left( {{{\sin }^2}A + {{\sin }^2}B + {{\sin }^2}C} \right) = {k^2}\left( {\sin A\sin C + \sqrt 3 \sin A\sin B} \right)\]
Cancel same terms from both sides of the equation
\[ \Rightarrow {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \sin A\sin C + \sqrt 3 \sin A\sin B\]
Now we can take \[\sin A\] common in RHS of the equation
\[ \Rightarrow {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \sin A\left( {\sin C + \sqrt 3 \sin B} \right)\]
Divide and multiply the bracket in RHS by 2
\[ \Rightarrow {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \sin A \times 2\left( {\dfrac{1}{2}\sin C + \dfrac{{\sqrt 3 }}{2}\sin B} \right)\]
We can write the terms in bracket in RHS as \[\dfrac{1}{2}\sin C + \dfrac{{\sqrt 3 }}{2}\sin B = \cos B\sin C + \cos C\sin B\]
\[ \Rightarrow \dfrac{1}{2} = \cos \dfrac{\pi }{3}\]and \[\dfrac{{\sqrt 3 }}{2} = \cos \dfrac{\pi }{6}\]
\[ \Rightarrow B = \dfrac{\pi }{3};C = \dfrac{\pi }{6}\]...................… (1)
Now from sum of interior angles property we have \[A + B + C = {180^ \circ }\]
Substitute the values of B and C from equation (2)
\[ \Rightarrow A + \dfrac{\pi }{3} + \dfrac{\pi }{6} = {180^ \circ }\]
Take LCM in LHS of the equation
\[ \Rightarrow A + \dfrac{{2\pi + \pi }}{6} = {180^ \circ }\]
\[ \Rightarrow A + \dfrac{{3\pi }}{6} = {180^ \circ }\]
Cancel same terms from numerator and denominator in fraction
\[ \Rightarrow A + \dfrac{\pi }{2} = {180^ \circ }\]
We know \[\pi = {180^ \circ }\]
\[ \Rightarrow A + \dfrac{{{{180}^ \circ }}}{2} = {180^ \circ }\]
Cancel same terms from numerator and denominator in fraction
\[ \Rightarrow A + {90^ \circ } = {180^ \circ }\]
Shift all constants to RHS of the equation
\[ \Rightarrow A = {180^ \circ } - {90^ \circ }\]
\[ \Rightarrow A = {90^ \circ }\]
So, in \[\vartriangle ABC\], angle A is a right angle.
From the definition of right triangle we know the triangle having one of its angles as the right angle is a right triangle.
\[ \Rightarrow \vartriangle ABC\] is a right angled triangle.
Now since the measures of the other two angles are not equal implies that the two sides of the triangle are unequal.
So, \[\vartriangle ABC\] is not an isosceles triangle
\[\therefore \vartriangle ABC\] is right angled and not isosceles triangle
\[\therefore \]Option C is correct
Note: Many students attempt to solve this question by applying interior angle property and writing third angle in form of other two angles, this is wrong approach as then we will have to apply trigonometric formulas to the sum of two angles and it will yield no result in this case. We use the value \[\sqrt 3 \] given to us and transform our solution into a trigonometric formula.
* The table that tells us some basic values of trigonometric functions at common angles is given as
* Law of sine states that in a triangle ABC the ratio of side of a triangle to the sine of opposite angle is same for all the sides of the triangle, i.e. if side a has opposite angle A, side b has opposite angle B and side c has opposite angle C, then we can write \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\] where k is some constant term.
* Isosceles triangle has two sides of equal length and the angles opposite to equal sides are equal in measure.
* Equilateral triangle has all its sides of equal length and all its angles of equal measure.
* Right angled triangle has one of its angles as a right angle i.e. \[{90^ \circ }\]
Complete step-by-step solution:
Given equation is \[{a^2} + {b^2} + {c^2} = ac + \sqrt 3 ab\]..................… (1)

We have a triangle ABC, where side A has opposite angle A, side B has opposite angle B and side c has opposite angle C. So we can apply sine rule in the triangle.
i.e. \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\]
On cross multiplication of terms we get
\[a = k\sin A;b = k\sin B;c = k\sin C\]
Substitute the values of ‘a’, ‘b’ and ‘c’ in equation (1)
\[ \Rightarrow {\left( {k\sin A} \right)^2} + {\left( {k\sin B} \right)^2} + {\left( {k\sin C} \right)^2} = \left( {k\sin A} \right)\left( {k\sin C} \right) + \sqrt 3 \left( {k\sin A} \right)\left( {k\sin B} \right)\]
Write the multiplication of terms on both sides of the equation
\[ \Rightarrow {k^2}{\sin ^2}A + {k^2}{\sin ^2}B + {k^2}{\sin ^2}C = {k^2}\sin A\sin C + \sqrt 3 {k^2}\sin A\sin B\]
Take constant term common on both sides of the equation
\[ \Rightarrow {k^2}\left( {{{\sin }^2}A + {{\sin }^2}B + {{\sin }^2}C} \right) = {k^2}\left( {\sin A\sin C + \sqrt 3 \sin A\sin B} \right)\]
Cancel same terms from both sides of the equation
\[ \Rightarrow {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \sin A\sin C + \sqrt 3 \sin A\sin B\]
Now we can take \[\sin A\] common in RHS of the equation
\[ \Rightarrow {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \sin A\left( {\sin C + \sqrt 3 \sin B} \right)\]
Divide and multiply the bracket in RHS by 2
\[ \Rightarrow {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \sin A \times 2\left( {\dfrac{1}{2}\sin C + \dfrac{{\sqrt 3 }}{2}\sin B} \right)\]
We can write the terms in bracket in RHS as \[\dfrac{1}{2}\sin C + \dfrac{{\sqrt 3 }}{2}\sin B = \cos B\sin C + \cos C\sin B\]
\[ \Rightarrow \dfrac{1}{2} = \cos \dfrac{\pi }{3}\]and \[\dfrac{{\sqrt 3 }}{2} = \cos \dfrac{\pi }{6}\]
\[ \Rightarrow B = \dfrac{\pi }{3};C = \dfrac{\pi }{6}\]...................… (1)
Now from sum of interior angles property we have \[A + B + C = {180^ \circ }\]
Substitute the values of B and C from equation (2)
\[ \Rightarrow A + \dfrac{\pi }{3} + \dfrac{\pi }{6} = {180^ \circ }\]
Take LCM in LHS of the equation
\[ \Rightarrow A + \dfrac{{2\pi + \pi }}{6} = {180^ \circ }\]
\[ \Rightarrow A + \dfrac{{3\pi }}{6} = {180^ \circ }\]
Cancel same terms from numerator and denominator in fraction
\[ \Rightarrow A + \dfrac{\pi }{2} = {180^ \circ }\]
We know \[\pi = {180^ \circ }\]
\[ \Rightarrow A + \dfrac{{{{180}^ \circ }}}{2} = {180^ \circ }\]
Cancel same terms from numerator and denominator in fraction
\[ \Rightarrow A + {90^ \circ } = {180^ \circ }\]
Shift all constants to RHS of the equation
\[ \Rightarrow A = {180^ \circ } - {90^ \circ }\]
\[ \Rightarrow A = {90^ \circ }\]
So, in \[\vartriangle ABC\], angle A is a right angle.
From the definition of right triangle we know the triangle having one of its angles as the right angle is a right triangle.
\[ \Rightarrow \vartriangle ABC\] is a right angled triangle.
Now since the measures of the other two angles are not equal implies that the two sides of the triangle are unequal.
So, \[\vartriangle ABC\] is not an isosceles triangle
\[\therefore \vartriangle ABC\] is right angled and not isosceles triangle
\[\therefore \]Option C is correct
Note: Many students attempt to solve this question by applying interior angle property and writing third angle in form of other two angles, this is wrong approach as then we will have to apply trigonometric formulas to the sum of two angles and it will yield no result in this case. We use the value \[\sqrt 3 \] given to us and transform our solution into a trigonometric formula.
* The table that tells us some basic values of trigonometric functions at common angles is given as
| Angles (in degrees) | ${0^ \circ }$ | ${30^ \circ }$ | ${45^ \circ }$ | ${60^ \circ }$ | ${90^ \circ }$ |
| sin | 0 | $\dfrac{1}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{{\sqrt 3 }}{2}$ | $1$ |
| cos | 1 | $\dfrac{{\sqrt 3 }}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{1}{2}$ | 0 |
| tan | 0 | $\dfrac{1}{{\sqrt 3 }}$ | 1 | $\sqrt 3 $ | Not defined |
| cosec | Not defined | 2 | \[\sqrt 2 \] | \[\dfrac{2}{{\sqrt 3 }}\] | 1 |
| sec | 1 | \[\dfrac{2}{{\sqrt 3 }}\] | \[\sqrt 2 \] | 2 | Not defined |
| cot | Not defined | $\sqrt 3 $ | 1 | \[\dfrac{1}{{\sqrt 3 }}\] | 0 |
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




