Question

In a $\vartriangle ABC$ and $\vartriangle DEF$, $\angle A = \angle D$, $\angle B = \angle E$ and $AB = EF$.Will the two triangles be congruent? Give reason.

Answer 1

Hint: To determine the congruence result for the respective triangles then we will be looking forward to the given information because the triangle will be congruent if two sides and one angle will be equal or two angle and one side be equal to get the information of the congruency of the triangle.

Complete step-by-step answer:
Let us consider the following triangle to check the information of the congruency

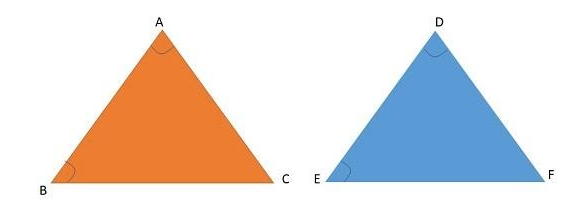
To prove the triangle to be congruent then in such case we need to determine the information
Two ways that proves the triangle to be congruent are
Side-Angle-Side
Then the two triangle the information are $\angle B = \angle E$
That means one angle is equal
Now, we need to show two sides be equal
But we have the information of one side $AB = EF$
That means the triangles is not congruent to one another by the property side-angle-side
Let us consider another type to prove the congruence
Angle-side-Angle
Two triangles are said to be congruent if they have same two angles and one side
Then the given information says that
$\angle A = \angle D$
Then the triangles have one same angle
$\angle B = \angle E$
Now, it is also provided that another angle is also equal that means two angles are equal
And it is also given that
$AB = EF$
One side of one triangle is equal to the other side of another triangle then in such case the required result is that the triangle is congruent to the other by the Angle-Side-Angle property.

Note: In the given question two triangles cannot be congruent by the property of SAS because the two sides of the triangle may or may not be equal because no such information is provided but it is congruent by angle-side-angle to know that the triangles are congruent.