Question

In a tug-of-war between the teams $A$ and $B$, the rope breaks at a point which is nearer to $A$. Then
A. A has applied more force
B. B has applied more force
C. A and B have applied same force
D. None has applied any force

Answer 1

Hint: We know that in a massless and taught rope, tension is the same throughout. But here, the rope has mass. We will solve the question by finding the variation of mass along the rope and then deciding the winner.

Complete step by step answer:
Let us first understand the variation of tension along a rope with mass $m$. Let its total length be $L$ and total mass be $m$. Let a force $F$ act on it from one end and let it be tied on the other end. This force produces an acceleration $a$ in the rope.The tension acting on a point at distance $x$ from the end is $T\left( x \right)$.

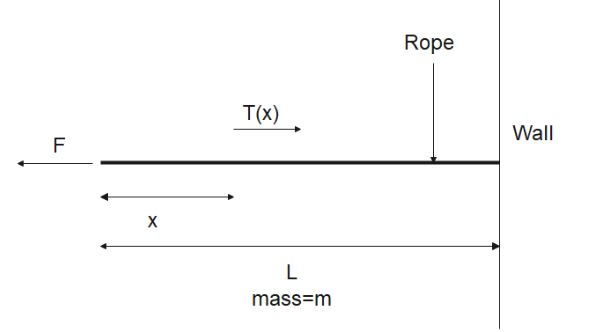
The force acting on the length $x$ is,
$Total{\kern 1pt} force - Tension{\kern 1pt} {\kern 1pt} at{\kern 1pt} {\kern 1pt} x = mass{\kern 1pt} {\kern 1pt} of{\kern 1pt} length{\kern 1pt} {\kern 1pt} x \times acceleration$ -----(i)
Mass of length $x$ $m(x) = m \times \dfrac{x}{L}$
Thus eq (i) becomes
$ \Rightarrow F - T\left( x \right) = m\dfrac{x}{L} \times a$

Since $F = m \times a$ , we have
$\Rightarrow ma - T\left( x \right) = m\dfrac{x}{L} \times a \\
\Rightarrow - T\left( x \right) = ma\dfrac{x}{L} - ma \\
\Rightarrow T\left( x \right) = ma - ma\dfrac{x}{L} \\
\Rightarrow T\left( x \right) = ma\left( {1 - \dfrac{x}{L}} \right) \\
\therefore T\left( x \right) = ma\left( {\dfrac{{L - x}}{L}} \right) \\ $
This equation shows us that tension is highest at the point of application of force and then decreases linearly. Thus, if the rope breaks nearer to one of the teams, it means that the team which is nearer to the breaking point has applied greater force. That greater force resulted in greater Tension and ultimately lead to the breaking of the rope

Therefore, option A is the correct answer.

Note: Here, the rope has been considered of uniform mass. If the mass of the rope was distributed haphazardly, then the answer would have been different. Also, the rope was considered inelastic here. If the rope had elastic properties, then the mechanics involved would have been much more complex.