Question

In a triangle \[\vartriangle PQR,\angle P={{60}^{\circ }}\] and \[\angle Q={{50}^{\circ }}\], which side of the triangle is the longest?
(a) PQ
(b) QR
(c) PR
(d) None

Answer 1

Hint: For solving this question you should know about the general properties of a triangle. In this problem we have given two angles and ask to find the biggest side. As we know that the property of a triangle states that the opposite arm of the biggest angle of a triangle is the biggest arm in that.

Complete step-by-step solution:
According to our question it is asked to find the biggest side of the \[\vartriangle PQR\] and \[\angle P={{60}^{\circ }}\] and \[\angle Q={{50}^{\circ }}\].
As we know that the angle of a triangle are always in a manner that their total will be \[{{180}^{\circ }}\]. So, angles of the triangles can be found if any two of them are given.
And the sides of triangle also depend on the angle of triangle. If any angle of triangle is the biggest then the opposite side from that angle will be the largest side in that triangle.
So, according to our question if we make a triangle PQR, then

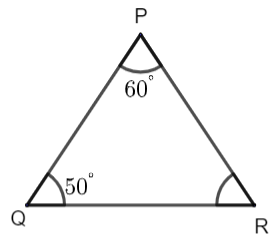
Here, \[\angle R=?\]
As we know that the property of angle sum of a triangle is that: \[\angle P+\angle Q+\angle R={{180}^{\circ }}\]
And here \[\angle P={{60}^{\circ }}\], \[\angle Q={{50}^{\circ }}\]
So, if we find \[\angle R\] then:
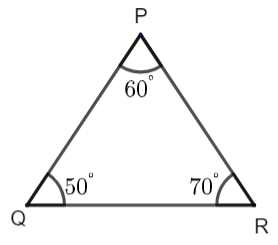
\[\begin{align}
  & \Rightarrow {{60}^{\circ }}+{{50}^{\circ }}+\angle R={{180}^{\circ }} \\
 & \Rightarrow \angle R={{180}^{\circ }}-{{110}^{\circ }} \\
 & \Rightarrow \angle R={{70}^{\circ }} \\
\end{align}\]
So, it is clear that the \[\angle R\] will be the greatest angle and the opposite side of this PQ is the longest side in \[\vartriangle PQR\].

Note: While solving this type of question we have to mind all the basic properties of a triangle and these properties will be used in it. If that asks for the angles of a triangle then solve it with the help of other angles and the sides. Because there will be no hint from that in this.