Question

In a triangle PQR, X and Y are 2 points on PQ and QR respectively. If $PQ=QR$ and $QX=QY$ show that $PX=RY$ .

Answer 1

Hint: First draw a picture and mark the lines which are equal. Now, by close observation using the lines which are equal tell the relation between lines required. By geometry’s basic properties we can say that when a point lies on a line segment, then it directly divides it into 2 parts. When we sum that 2 parts length together the result obtained will be the length of the whole old line segment. Using this property, divide the line segment in the question and then solve it as a normal algebraic equation.
Complete step-by-step answer:
Triangle: It is a 2-dimensional figure with 3 sides. It is a closed figure. It is represented by 2 length (generally) one is height and the other one is base length.
Given in question 2 sides are equal. Hence, it is an isosceles triangle.
Aim: to prove lengths of PX and RY are equal.
Given: $PQ=QR$ , $QX=QY$
First, we need to construct an isosceles triangle.

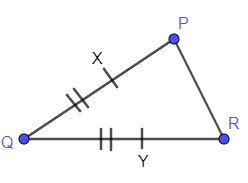
Drawing two line-segments with a point in common, angle doesn’t matter but lengths must be the same.
Mark the common point as Q and the remaining two points as P and R.
So, now we got $PQ=QR$ . Next join P and R to make a triangle.
Take 2 points X, Y at equal distance from Q on PQ and PR respectively.
Now we also got $QX=QY$
As X, Y lies on PQ, QR respectively, we can write them as:
$PQ=PX+QX$ , $QR=QY+RY$
As we know $PQ=QR$ , equating these both equations, we get
$PX+QX=QY+RY$
By cancelling the common terms, (We know $QX=QY$ ), we get
$PX=RY$
By the above equation, we can say the length of line segments PX and RY are equal.
Hence, proved.
Note: Here students must be careful while writing the equations on line segments as if you change one variable the whole proof may conclude another equation which may be wrong.