Question

In a triangle $PQR$, $P$ is the largest angle and $\cos P = \dfrac{1}{3}$. Further, the incircle of the triangle touches the side $PQ,QR$ and $RP$ at $N,L,M$ respectively, such that the lengths $PN,QL,RM$ respectively. Then a possible length of the side of the triangle is/are:
$\left( {\text{A}} \right)$$16$,$18$,$20$
$\left( {\text{B}} \right)$$18,20,22$
$\left( {\text{C}} \right)$$24,26,28$
$\left( {\text{D}} \right)$$22,24,26$

Answer 1

Hint: Here we have to assume that since $PN,QL,RM$ are consecutive even integers so we can write $PN = 2k - 2,QL = 2k,RM = 2k + 2$, where value of $k$ is greater than $1$. Since from an exterior point a tangent has touched the circle, therefore the length of the sides are also equal.

Formula used: $\cos P = \dfrac{{b_{}^2 + c_{}^2 - a_{}^2}}{{2bc}}$
$(a + b)_{}^2 = a_{}^2 + 2ab + b_{}^2$ and $(a - b)_{}^2 = a_{}^2 - 2ab + b_{}^2$

Complete step-by-step solution:
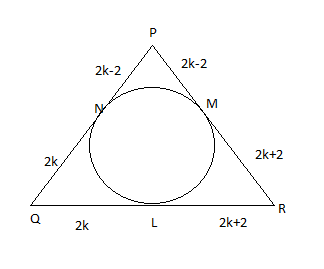
From the above diagram we can write that the sum of the three of the triangle will be its perimeter
So $2(2k - 2) + 2(2k) + 2(2k + 2) = 2s$ where $2s$ represents the perimeter of the triangle because $s$ represents a semi-perimeter.
$ \Rightarrow 4k - 4 + 4k + 4k + 4 = 2s$
On some simplification we get,
$ \Rightarrow 2s = 12k$
Now by division we get
$ \Rightarrow s = \dfrac{{12k}}{2} = 6k$
From the above diagram we can write that the value of $s - a = 2k - 2$ where $a,b,c$ are the length of sides of the triangle
So, by substituting the value of $s$ in the above equation we get-
$ \Rightarrow 6k - a = 2k - 2$
Now we have to add the variable k and we get the value of $a = 4k + 2$
Again from the diagram we can write that the value of $s - b = 2k$
Substituting the value of $s$ in the above equation we get-
$ \Rightarrow 6k - b = 2k$
Therefore value of $b = 4k$
Again, we can write that value of $s - c = 2k + 2$
Now by substituting the value of $s$ in the above equation we get-
$ \Rightarrow 6k - c = 2k + 2$
Therefore the value of $c = 4k - 2$
Now it is stated in the question that $\cos P = \dfrac{1}{3}$
Now we have to apply the formula of $\dfrac{{b_{}^2 + c_{}^2 - a_{}^2}}{{2bc}} = \dfrac{1}{3}$
Substituting the values of $a,b,c$ in the above equation we get-
$ \Rightarrow \dfrac{{(4k)_{}^2 + (4k - 2)_{}^2 - (4k + 2)_{}^2}}{{2(4k)(4k - 2)}} = \dfrac{1}{3}$
Now by applying the formula of $(a + b)_{}^2 = a_{}^2 + 2ab + b_{}^2$and $(a - b)_{}^2 = a_{}^2 - 2ab + b_{}^2$we get-
$ \Rightarrow \dfrac{{16k_{}^2 + (16k_{}^2 + 2 \times 4k \times 2 + 4) - (16k_{}^2 - 16k + 4)}}{{4k(4k - 2)}} = \dfrac{1}{3}$
Now we have to multiply the bracket terms and we get
\[ \Rightarrow \dfrac{{16k_{}^2 + (16k_{}^2 + 16k + 4) - (16k_{}^2 - 16k + 4)}}{{(32{k^2} - 16k)}} = \dfrac{1}{3}\]
On simplifying the terms we get,
\[ \Rightarrow \dfrac{{16k_{}^2 + 16k_{}^2 + 16k + 4 - 16k_{}^2 + 16k - 4)}}{{(32{k^2} - 16k)}} = \dfrac{1}{3}\]
Cancel the same terms and doing cross multiplication we get-
$ \Rightarrow 16k_{}^2 - 32k = \dfrac{1}{3}(32k_{}^2 - 16k)$
On dividing $16$ on both the sides we get-
$ \Rightarrow k_{}^2 - 2k = \dfrac{1}{3}(2k_{}^2 - k)$
Now by doing cross multiplication
$ \Rightarrow 3k_{}^2 - 6k = 2k_{}^2 - k$
On simplifying the terms we get,
So, $k_{}^2 = 5k$
Hence the value of $k$ is $5$.
Therefore the length of the side $a = 4k + 2 = 4.5 + 2 = 22$, since the value of $k$ is $5$
Length of side $b = 4k = 4.5 = 20$
Length of side c$ = 4 \times k - 2 = 4 \times 5 - 2 = 18$

Thus, the correct option is B.

Note: A $2s$ represents perimeter of the triangle
Triangles come in many shapes and sizes according to the angles of their corners.
Some triangles, called similar triangles, have the same angles but different sides’ lengths.
This changes the ratio of the triangle, making it bigger or smaller, without changing the degree of its three angles.