Question

In a triangle ABC with \[\angle A\angle B\angle C\], points D, E, F are on the interior segments BC, CA, AB respectively. Which of the following triangles cannot be similar to the triangle ABC.

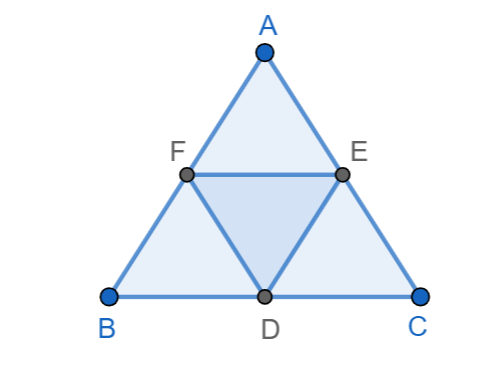
A. Triangle ABD
B. Triangle BCE
C. Triangle CAF
D. Triangle DEF

Answer 1

Hint: In this problem, we have to find the triangle which is not similar to the triangle ABC. We can start by checking the similarities of the triangles by checking whether their three sides are in proportion or not. We can write the three sides of both triangles in ratios and check whether they satisfy the same proportion rule. If they don’t satisfy that means they are not similar triangles and we will get the answer.

Complete step by step solution:
We know that the given triangle ABC with \[\angle A\angle B\angle C\], points D, E, F are on the interior segments BC, CA, AB respectively.

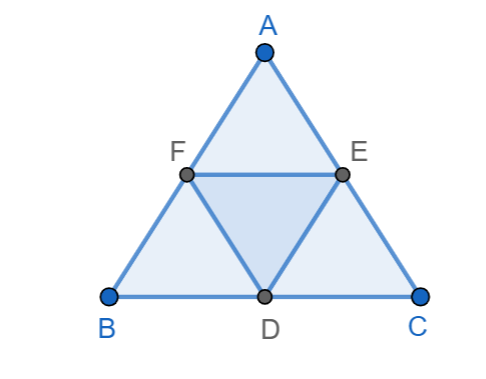
Now we can find the similarities of the triangle.
We can take the first option A to check for the similarity, we get
\[\Delta ABC\sim \Delta ABD\]
We know that the ratio of the corresponding sides should be equal.
We get,
\[\dfrac{AB}{AB}=\dfrac{BC}{BD}=\dfrac{AC}{AD}\]
We can now simplify the above step, we get
\[\Rightarrow \dfrac{1}{1}=\dfrac{BC}{BD}=\dfrac{AC}{AD}\]
We can see that from the above ratio,
\[BC=BD\]
Which is not possible, as D lies between BC and \[BC>BD\].
So, \[\Delta ABD\] is not similar to \[\Delta ABC\] .
Therefore, the option A. Triangle ABD is correct which is not similar to triangle ABC.
So, the correct answer is “Option A”.

Note: We should know that similar triangles having the same shape but different sizes, for two triangles to be similar their corresponding angles should be congruent and the corresponding sides should be in proportion. The symbol used to denote similarity of triangles is \[\sim \].