Question

In a triangle ABC, side AB is extended beyond B, side BC is extended beyond C and side CA is extended beyond A. What is the sum of the three exterior angles.
$\begin{align}
  & a){{270}^{\circ }} \\
 & b){{305}^{\circ }} \\
 & c){{360}^{\circ }} \\
 & d){{540}^{\circ }} \\
\end{align}$

Answer 1

Hint: Now first the triangle we will extend the arms and form the required figure. Now write the equation of linear angles for each arm that is the sum of linear angles is 180 degrees. Hence we will get three equations. Add all three equations and use the fact that the sum of all interior angles of triangles is equal to 180 degrees. Hence we will get the sum of all exterior angles.

Complete step-by-step answer:
Now first let us draw the triangle ABC, side AB is extended beyond B let us say till P, side BC is extended beyond C let us say till Q and side CA is extended beyond A let us say till R.

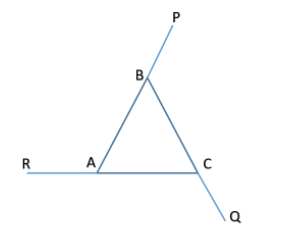
Now first let us write all the linear angles
We know that the sum of linear angles is equal to ${{180}^{\circ }}$
 $\begin{align}
  & \angle ABC+\angle PBC={{180}^{\circ }}.................(1) \\
 & \angle ACB+\angle ACQ={{180}^{\circ }}.................(2) \\
 & \angle CAB+\angle RAB={{180}^{\circ }}.................(3) \\
\end{align}$
Now we also know that the sum of angles in a triangle is equal to \[{{180}^{\circ }}\]
Hence we have
\[\angle ABC+\angle ACB+\angle CAB={{180}^{\circ }}.............(4)\]
Now let us add equation (1), equation (2) and equation (3) $\angle ABC+\angle PBC+\angle ACB+\angle ACQ+\angle CAB+\angle RAB={{180}^{\circ }}+{{180}^{\circ }}+{{180}^{\circ }}$
Now let us group alternate terms together.
$\left( \angle ABC+\angle ACB+\angle CAB \right)+\angle PBC+\angle ACQ+\angle RAB={{540}^{\circ }}$
Now from equation (4) let us substitute the value of $\angle ABC+\angle ACB+\angle CAB$
Hence we will get
$\left( {{180}^{\circ }} \right)+\angle PBC+\angle ACQ+\angle RAB={{540}^{\circ }}$
Now let us subtract 180 degrees on RHS and LHS.
Hence we get
\[\begin{align}
  & \angle PBC+\angle ACQ+\angle RAB={{540}^{\circ }}-{{180}^{\circ }} \\
 & \Rightarrow \angle PBC+\angle ACQ+\angle RAB={{360}^{\circ }} \\
\end{align}\]
But \[\angle PBC\] is exterior angle of AB, \[\angle ACQ\] is exterior angle of BC and \[\angle RAB\] is exterior angle of AC.
Hence we get the sum of all exterior angles of triangles is equal to ${{360}^{\circ }}$

Note: Note that this is a well-known result that the sum of exterior angles of any polygon is 360 degrees. Now the sum of linear angles is 180 degrees and the sum of all interior angles of triangles is 180 degrees. Hence not to be confused among these, especially in exterior angle and interior angle.