Question

In a triangle ABC ,\[{\rm{B}} = 90^\circ \]and \[a + b = 4\]. The area of the triangle is maximum when C, is
A.\[\dfrac{\pi }{4}\]
B.\[\dfrac{\pi }{6}\]
C.\[\dfrac{\pi }{3}\]
D.None of these

Answer 1

Hint: Here firstly we have to find the third side of the right triangle using the Pythagoras theorem. Then we have to find out the value of the area of the triangle and squaring on both sides. We will then substitute the value of the third side to make a relation between the area and side \[a\]. We will use the fact that for an expression to be maximum its differentiation must be equal to zero. Solving the equation further, we will get all the sides of the triangle and then by using the trigonometric function we will get the value of angle C.

Formula used: We will use the formula of area of the triangle\[ = \dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height}}\].

Complete step by step solution:
Let us assume a, b, c be the sides of the right triangle with right angle at point B.

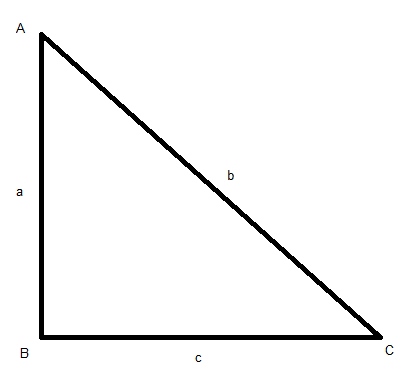
It is given that value of \[a + b = 4\]
Now we have to use the Pythagoras theorem to find the value of the third side i.e. c in terms of side a.
Therefore we get
\[ \Rightarrow {a^2} + {c^2} = {b^2}\]
\[ \Rightarrow {c^2} = {b^2} - {a^2}\]
By using this identity \[{a^2} - {b^2} = (a + b)(a - b)\], we get
\[ \Rightarrow {c^2} = (b + a)(b - a)\]
Substituting the value of\[a + b = 4\], we get
\[ \Rightarrow {c^2} = (4)(4 - a - a) = 8(2 - a)\]
Now we have to find out the area of the triangle ABC.
Area of the triangle, A\[ = \dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height = }}\dfrac{1}{2} \times a \times c\]
Squaring on the both side, we get
\[ \Rightarrow {{\rm{A}}^2} = \dfrac{1}{4}{a^2}{c^2}\]
Now substituting the value of \[{c^2}\] in the above equation, we get
\[ \Rightarrow {{\rm{A}}^2} = \dfrac{1}{4}{a^2}.8(2 - a) = 2(2{a^2} - {a^3})\]
Now, we know that for an expression to be maximum its differentiation must be equal to zero. So we ill differentiate this area square with respect to a and equating it to 0. Then by solving this we will get the value of all the sides of the triangle, we get
\[\dfrac{{d{{\rm{A}}^2}}}{{da}} = 0 = 2(4a - 3{a^2})\]
Now by solving this we will get the value of a, we get
\[a = \dfrac{4}{3}\]
Now we know the value of a. we can calculate the value of side b and c. therefore we get
\[b = \dfrac{8}{3},c = \dfrac{4}{{\sqrt 3 }}\]
Now by using the trigonometry function we will get the value of C. Therefore
\[\tan C = \dfrac{c}{a} = \dfrac{{\dfrac{4}{{\sqrt 3 }}}}{{\dfrac{4}{3}}} = \dfrac{3}{{\sqrt 3 }} = \sqrt 3 \]
We know that the value of the tan function at angle \[\dfrac{\pi }{3}\]is equals to \[\sqrt 3 \]
Therefore, the area of the triangle is maximum when C is\[\dfrac{\pi }{3}\].
Hence, option C is the correct option.

Note: Here we have to make sure that we have to convert the area of the triangle into a single variable to make the equation more simplified when it gets differentiated. We should know that for an expression or some shape to be maximum its differentiation must be equal to zero. If this condition does not satisfy then the shape or expression is not maximum at that value.