Question

In a triangle ABC, right angled at B, AB=24cm, BC=7cm. Determine
$
  (i){\text{ sinA,cosA}} \\
  {\text{(ii)sinC,cosC}} \\
 $

Answer 1

Hint – In this question first of all use the Pythagoras theorem to get the value of side AC, that is ${\left( {{\text{AC}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{BC}}} \right)^2}$, then use the concept that in triangle ABC when we consider angle A the perpendicular become BC and base become AB and hypotenuse remains same and we consider angle C the perpendicular become AB and base become BC and hypotenuse remains same. This will help get the values of the respective trigonometric angles.
Complete step-by-step answer:

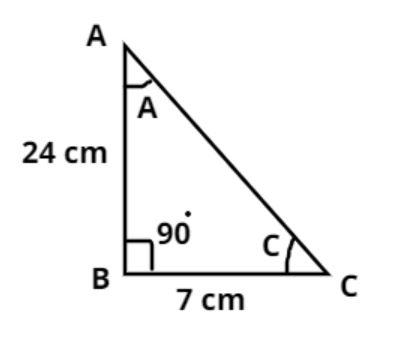
The pictorial representation of the above problem is shown having right angle at B as shown in the figure.
It is given that AB = 24 cm, and BC = 7 cm.
Now apply Pythagoras theorem in triangle ABC we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{BC}}} \right)^2}$
Now substitute the value we have,
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} = {\left( {24} \right)^2} + {\left( 7 \right)^2} = 576 + 49 = 625 = {\left( {25} \right)^2}$
$ \Rightarrow AC = 25$ cm.
$\left( i \right)\sin A,\cos A$
Now as we know that sine is the ratio of perpendicular to hypotenuse.
So in triangle ABC when we consider angle A the perpendicular becomes BC and base becomes AB and hypotenuse remains the same.
$ \Rightarrow \sin A = \dfrac{{BC}}{{AC}} = \dfrac{7}{{25}}$
And cosine is the ratio of base to hypotenuse.
$ \Rightarrow \cos A = \dfrac{{AB}}{{AC}} = \dfrac{{24}}{{25}}$
$\left( {ii} \right)\sin C,\cos C$
Now as we know that sine is the ratio of perpendicular to hypotenuse.
So in triangle ABC when we consider angle C the perpendicular becomes AB and base becomes BC and hypotenuse remains the same.
$ \Rightarrow \sin C = \dfrac{{AB}}{{AC}} = \dfrac{{24}}{{25}}$
And cosine is the ratio of base to hypotenuse.
$ \Rightarrow \cos C = \dfrac{{BC}}{{AC}} = \dfrac{7}{{25}}$
So this is the required answer.

Note – It is advised to remember the direct formula for basic trigonometric ratios like $\sin \theta = \dfrac{P}{H},\cos \theta = \dfrac{B}{H},\tan \theta = \dfrac{P}{B}$ and $\cos ec\theta = \dfrac{H}{P},\sec \theta = \dfrac{H}{B},\cot \theta = \dfrac{B}{P}$. The trick point while considering different angles in a triangle is that the hypotenuse remains the same always however for the angles that are non-90 degrees the side which is exactly in front of it acts as perpendicular.