
In a triangle ABC $ {r_1} = 39,{r_2} = 70 $ and $ \angle C = \dfrac{\pi }{2} $ then, if $ \vartriangle = {P_1}{P_2}{P_3}{P_4}{P_5} $ where $ {P_1},{P_2},{P_3},{P_4},{P_5} $ are primes then max if $ \left\{ {{P_1},{P_2},{P_3},{P_4},{P_5}} \right\} $ is
A) 7
B) 5
C) 13
D) 17
Answer
587.7k+ views
Hint: In a triangle when the length of two sides and one angle is given, then the area of the triangle will be $ \dfrac{{ab\sin C}}{2} $ where a, b are the lengths of the given sides and C is the given angle. After finding the area of the triangle, prime factorize the value of the area which gives the highest prime number value.
Complete step-by-step answer:
We are given a triangle ABC, where the lengths of the sides is $ {r_1} = 39,{r_2} = 70 $ and length of the included angle is $ \angle C = \dfrac{\pi }{2} $
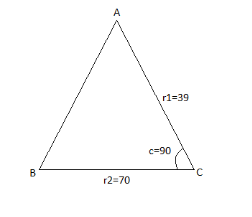
Area of the triangle ABC is $ \dfrac{{ab\sin C}}{2} $ , where a=AC=39, b=BC=70 and C= $ \angle C = \dfrac{\pi }{2} $
Area of ABC is
$
= \dfrac{{39 \times 70 \times \sin \dfrac{\pi }{2}}}{2} \\
\sin \dfrac{\pi }{2} = 1 \\
= \dfrac{{39 \times 70 \times 1}}{2} \\
= 39 \times 35 \\
= 1365 \\
$
Area of the triangle ABC is 1365 square units.
Prime factorize 1365. 2 is the first prime but 1365 is an odd number so it is not divisible by 2. So start from 3.
1365 can be written as 3 times 455.
$ 1365 = 3 \times 455 $
455 can be written as 5 times 91
$ 1365 = 3 \times 5 \times 91 $
91 can be written as 7 times 13
$ 1365 = 3 \times 5 \times 7 \times 13 $
13 is a prime number, so there will be no further factorization.
1365 can be written as the product of 3, 5, 7 and 13. The maximum of 3, 5, 7 and 13 is 13.
Therefore, from among the options given in the question Option C is correct.
So, the correct answer is “Option C”.
Note: When two sides and an angle are given for a triangle, then the method of calculating the area is known as the side-angle-side method. And the area $ \dfrac{{ab\sin C}}{2} $ can be used in any triangle not just for right angled triangles.
Complete step-by-step answer:
We are given a triangle ABC, where the lengths of the sides is $ {r_1} = 39,{r_2} = 70 $ and length of the included angle is $ \angle C = \dfrac{\pi }{2} $
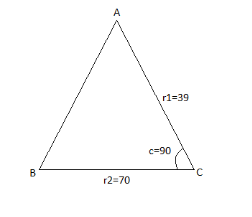
Area of the triangle ABC is $ \dfrac{{ab\sin C}}{2} $ , where a=AC=39, b=BC=70 and C= $ \angle C = \dfrac{\pi }{2} $
Area of ABC is
$
= \dfrac{{39 \times 70 \times \sin \dfrac{\pi }{2}}}{2} \\
\sin \dfrac{\pi }{2} = 1 \\
= \dfrac{{39 \times 70 \times 1}}{2} \\
= 39 \times 35 \\
= 1365 \\
$
Area of the triangle ABC is 1365 square units.
Prime factorize 1365. 2 is the first prime but 1365 is an odd number so it is not divisible by 2. So start from 3.
1365 can be written as 3 times 455.
$ 1365 = 3 \times 455 $
455 can be written as 5 times 91
$ 1365 = 3 \times 5 \times 91 $
91 can be written as 7 times 13
$ 1365 = 3 \times 5 \times 7 \times 13 $
13 is a prime number, so there will be no further factorization.
1365 can be written as the product of 3, 5, 7 and 13. The maximum of 3, 5, 7 and 13 is 13.
Therefore, from among the options given in the question Option C is correct.
So, the correct answer is “Option C”.
Note: When two sides and an angle are given for a triangle, then the method of calculating the area is known as the side-angle-side method. And the area $ \dfrac{{ab\sin C}}{2} $ can be used in any triangle not just for right angled triangles.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




