Question

In a triangle ABC $\dfrac{{{r}_{1}}+{{r}_{2}}}{1+\cos C}$ is equal to?
(a) $\dfrac{2ab}{c\Delta }$
(b) $\dfrac{\left( a+b \right)}{c\Delta }$
(c) $\dfrac{abc}{2\Delta }$
(d) $\dfrac{abc}{{{\Delta }^{2}}}$

Answer 1

Hint: Assume the given expression $\dfrac{{{r}_{1}}+{{r}_{2}}}{1+\cos C}$ as E. Here, ${{r}_{1}}$ and ${{r}_{2}}$ are radii of ex – circles of triangle ABC opposite the vertex A and B respectively. Now, substitute the value of relations ${{r}_{1}}=\dfrac{\Delta }{\left( s-a \right)}$ and ${{r}_{2}}=\dfrac{\Delta }{\left( s-b \right)}$ in the assumed expression E, where s is the semi – perimeter given as $s=\dfrac{a+b+c}{2}$ while a, b and c are the sides opposite to the vertex A, B and C of the triangle respectively. Use the formula for the area of the triangle given as $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to simplify the expression and get the answer.

Complete step by step solution:
Here we have been provided with a triangle ABC and we have to determine the value of the expression $\dfrac{{{r}_{1}}+{{r}_{2}}}{1+\cos C}$ in terms of a, b, c and $\Delta $. First we need to understand the symbols used here.
Now, let us assume the given expression as E, so we have,
$\Rightarrow E=\dfrac{{{r}_{1}}+{{r}_{2}}}{1+\cos C}$
Here, ${{r}_{1}}$ and ${{r}_{2}}$ are radii of ex – circles of triangle ABC opposite the vertex A and B respectively. Ex – circles are formed by the three sides of a triangle in which two sides are extended and with the condition that all the three sides are working as tangents. An illustration is shown below.

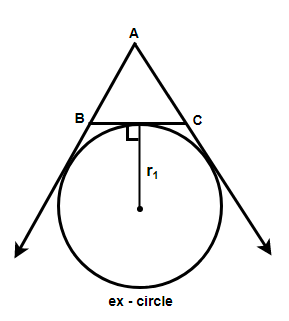
The values of ${{r}_{1}}$ and ${{r}_{2}}$ is given by the relations: ${{r}_{1}}=\dfrac{\Delta }{\left( s-a \right)}$ and ${{r}_{2}}=\dfrac{\Delta }{\left( s-b \right)}$ where $\Delta $ is the area of the triangle and s is the semi – perimeter given as $s=\dfrac{a+b+c}{2}$. So substituting the values of ${{r}_{1}}$ and ${{r}_{2}}$ in the expression E we get,
$\begin{align}
  & \Rightarrow E=\dfrac{\dfrac{\Delta }{\left( s-a \right)}+\dfrac{\Delta }{\left( s-b \right)}}{1+\cos C} \\
 & \Rightarrow E=\dfrac{\Delta \left( \dfrac{1}{\left( s-a \right)}+\dfrac{1}{\left( s-b \right)} \right)}{1+\cos C} \\
 & \Rightarrow E=\dfrac{\Delta \left( 2s-\left( a+b \right) \right)}{\left( s-a \right)\left( s-b \right)\left( 1+\cos C \right)} \\
\end{align}$
Using the cosine formula $\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$ and the semi perimeter formula $s=\dfrac{a+b+c}{2}$ we get,
\[\begin{align}
  & \Rightarrow E=\dfrac{\Delta \left( \left( a+b+c \right)-\left( a+b \right) \right)}{\left( s-a \right)\left( s-b \right)\left( 1+\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} \right)} \\
 & \Rightarrow E=\dfrac{\Delta \times c\times 2ab}{\left( s-a \right)\left( s-b \right)\left( 2ab+{{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)} \\
\end{align}\]
Using the algebraic identity ${{x}^{2}}+{{y}^{2}}-2xy={{\left( x+y \right)}^{2}}$ we get,
\[\Rightarrow E=\dfrac{2abc\Delta }{\left( s-a \right)\left( s-b \right)\left( {{\left( a+b \right)}^{2}}-{{c}^{2}} \right)}\]
Using the algebraic identity ${{x}^{2}}-{{y}^{2}}=\left( x+y \right)\left( x-y \right)$ we get,
\[\begin{align}
  & \Rightarrow E=\dfrac{2abc\Delta }{\left( s-a \right)\left( s-b \right)\left( a+b+c \right)\left( a+b-c \right)} \\
 & \Rightarrow E=\dfrac{2abc\Delta }{\left( s-a \right)\left( s-b \right)\times 2s\left( a+b-c \right)} \\
\end{align}\]
Multiplying the numerator and denominator with $\left( s-c \right)$ we get,
\[\Rightarrow E=\dfrac{abc\Delta \times \left( s-c \right)}{s\left( s-a \right)\left( s-b \right)\left( s-c \right)\left( a+b-c \right)}\]
We know that the area of a triangle is given as $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ so substituting this in the above relation we get,
\[\Rightarrow E=\dfrac{abc\Delta \times \left( s-c \right)}{{{\Delta }^{2}}\left( a+b-c \right)}\]
Again substituting the value $s=\dfrac{a+b+c}{2}$ in the numerator and simplifying we get,
\[\begin{align}
  & \Rightarrow E=\dfrac{abc\times \left( \dfrac{a+b+c}{2}-c \right)}{\Delta \left( a+b-c \right)} \\
 & \Rightarrow E=\dfrac{abc\times \left( \dfrac{a+b-c}{2} \right)}{\Delta \left( a+b-c \right)} \\
 & \therefore E=\dfrac{abc}{2\Delta } \\
\end{align}\]
Hence option (c) is the correct answer.

Note: Remember that there are three ex – circles of a triangle, one in – circle and one circum – circle. So there are three ex – radii denoted with ${{r}_{1}},{{r}_{2}}$ and \[{{r}_{3}}\], one in – radius given as $r=\dfrac{\Delta }{s}$ and one circum – radius given as $R=\dfrac{abc}{4\Delta }$. Remember all the formulas of the topic properties of triangle as they will not be proved everywhere but directly used.