Question

In a triangle ABC, AD is the bisector of angle A, meeting side BC at D.
(i)If BD = 2.5 cm, AB = 5 cm and AC = 4.2 cm, find DC.
(ii) If BD = 2 cm, AB = 5 cm and DC = 3 cm, find AC.
(iii) If AB = 3.5 cm, AC = 4.2 cm and DC = 2.8 cm, find BD.
(iv) If AB = 10 cm, AC = 14 cm and BC =6 cm, find BD And DC.
(v) If AC = 4.2 cm, DC = 6 cm and BC = 10 cm, find AB.
(vi) If AB = 5.6 cm, AC = 6 cm and DC = 3 cm, find BC.
(vii) If AB = 5.6 cm, BC = 6 cm and BD = 3.2 cm, find AC.
(viii) If AB = 10 cm, AC = 6 cm and BC = 12 cm, find BD And DC.

Answer 1

Hint: Use the Angle Bisector theorem, An angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other two sides of triangle.
Here:
\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]

Angle bisector is a line which bisects the internal angle exactly by half.
So from above figure we can say
The value of angle BAD is equal to the value of angle DAC. As the bisector is the ray in the interior of an angle forming two congruent angles.
We need to find AC. So using the condition that AD is a internal angular bisector we will derive a relation for AC.

Complete step-by-step answer:
Now we take a different condition to prove angle bisector theorem.
Let BD be the angle bisector of B. As shown in the figure.

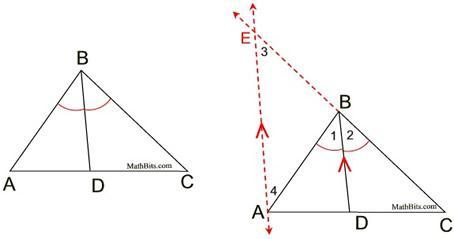
The angles 1 and 2 are equal. As the line BD is given to be internal angular bisector of angle B.
Draw an auxiliary line through A parallel to line BD as shown in figure. AS said in parallel postulate: Through a point not on a line there is only line parallel to the given line.
The angles 2 and 3 are equal, because if 2 parallel lines are cut by a transversal, the corresponding angles are congruent.
The angles 1 and 4 are equal, because if 2 parallel lines are cut by a transversal, the corresponding angles are congruent.
The angles 3 and 4 are also equal, because 1 and 2 are equal.
Side Splitter Theorem: If a line is parallel to one side of triangle and intersects the other 2 sides, it divides the sides proportionally.
By above theorem, we get:
\[\dfrac{AD}{CD}=\dfrac{EB}{CB}\]
Side AB is congruent to side EB, because if 2 triangles are congruent the sides opposite angles are congruent.
AB = EB, because congruent segments have equal lengths.
By substituting, we get:
\[\dfrac{AD}{CD}=\dfrac{AB}{CB}\]
This proves angle bisector theorem.
Now coming to our question:
The AD is angle bisector.
So the angle bisector theorem here turns out to be:
(i)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
In question it is given:
If BD = 2.5 cm, AB = 5 cm and AC = 4.2 cm
Substituting above values, we get:
\[\dfrac{2.5}{DC}=\dfrac{5}{4.2}\]
By simplifying, we get:
\[DC=\dfrac{4.2}{2}\]
DC = 2.1cm
Therefore the length of side DC is 2.1 cm.
(ii)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
In question it is given:
If BD = 2 cm, AB = 5 cm and DC = 3 cm
Substituting above values, we get:
\[\dfrac{2}{3}=\dfrac{5}{AC}\]
By simplifying, we get:
\[AC=\dfrac{15}{2}\]
AC = 7.5cm
Therefore the length of side AC is 7.5 cm.
(iii)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
In question it is given:
If AB = 3.5 cm, AC = 4.2 cm and DC = 2.8 cm
Substituting above values, we get:
\[\dfrac{BD}{2.8}=\dfrac{3.5}{4.2}\]
By simplifying, we get:
\[BD=\dfrac{7}{3}\]
BD = 2.33 cm
Therefore the length of side BD is 7.5 cm.
(iv)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
By adding 1 on both sides, we get:
\[\begin{align}
  & \dfrac{BD}{DC}+1=\dfrac{AB}{AC}+1 \\
 & \dfrac{BD+DC}{DC}=\dfrac{AB+AC}{AC} \\
\end{align}\]
We know:
BD + DC = BC
By substituting this, we get:
\[\dfrac{BC}{DC}=\dfrac{AB+AC}{AC}\]
In question it is given:
If AB = 10 cm, AC = 14 cm and BC =6 cm
Substituting above values, we get:
\[\begin{align}
  & \dfrac{6}{DC}=\dfrac{10+14}{14} \\
 & \dfrac{6}{DC}=\dfrac{24}{14} \\
\end{align}\]
By simplifying, we get:
\[DC=\dfrac{7}{2}\]
DC = 3.5 cm
For finding BD,
We know:
BD + DC = BC
By substituting, we get:
BD = 6 cm - 3.5 cm = 2.5 cm
Therefore the length of side BD and DC are 2.5 cm and 3.5 cm respectively.
(v)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
By adding 1 on both sides, we get:
\[\begin{align}
  & \dfrac{BD}{DC}+1=\dfrac{AB}{AC}+1 \\
 & \dfrac{BD+DC}{DC}=\dfrac{AB+AC}{AC} \\
\end{align}\]
We know:
BD + DC = BC
By substituting this, we get:
\[\dfrac{BC}{DC}=\dfrac{AB+AC}{AC}\]
In question it is given:
If AC = 4.2 cm, DC = 6 cm and BC = 10 cm
Substituting above values, we get:
\[\dfrac{10}{6}=\dfrac{AB+4.2}{4.2}\]
By simplifying, we get:
\[AB=\dfrac{42}{6}-4.2\]
AB = 2.8 cm
Therefore the length of side AB is 2.8 cm.
(vi)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
By adding 1 on both sides, we get:
\[\begin{align}
  & \dfrac{BD}{DC}+1=\dfrac{AB}{AC}+1 \\
 & \dfrac{BD+DC}{DC}=\dfrac{AB+AC}{AC} \\
\end{align}\]
We know:
BD + DC = BC
By substituting this, we get:
\[\dfrac{BC}{DC}=\dfrac{AB+AC}{AC}\]
In question it is given:
If AB = 5.6 cm, AC = 6 cm and DC = 3 cm
Substituting above values, we get:
\[\dfrac{BC}{3}=\dfrac{5.6+6}{6}\]
By simplifying, we get:
\[BC=\dfrac{11.6}{2}\]
BC = 5.8 cm
Therefore the length of side BC is 5.8 cm.
(vii)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
By adding 1 on both sides, we get:
\[\begin{align}
  & \dfrac{BD}{DC}+1=\dfrac{AB}{AC}+1 \\
 & \dfrac{BD+DC}{DC}=\dfrac{AB+AC}{AC} \\
\end{align}\]
We know:
BD + DC = BC
By substituting this, we get:
\[\dfrac{BC}{DC}=\dfrac{AB+AC}{AC}\]
In question it is given:
If AB = 5.6 cm, BC = 6 cm and BD = 3.2 cm
BC = BD + DC
DC = BC – BD
DC = 6 – 3.2
DC = 2.8 cm
Substituting above values, we get:
\[\dfrac{6}{2.8}=\dfrac{5.6+AC}{AC}\]
By simplifying, we get:
6.AC = (15.68) + 2.8AC
3.2 AC = 15.68
\[AC=\dfrac{15.68}{3.2}\]
AC = 4.9 cm
Therefore the length of side AC is 4.9 cm.
(viii)\[\dfrac{BD}{DC}=\dfrac{AB}{AC}\]
By adding 1 on both sides, we get:
\[\begin{align}
  & \dfrac{BD}{DC}+1=\dfrac{AB}{AC}+1 \\
 & \dfrac{BD+DC}{DC}=\dfrac{AB+AC}{AC} \\
\end{align}\]
We know:
BD + DC = BC
By substituting this, we get:
\[\dfrac{BC}{DC}=\dfrac{AB+AC}{AC}\]
In question it is given:
If AB = 10 cm, AC = 6 cm and BC = 12 cm,
Substituting above values, we get:
\[\begin{align}
  & \dfrac{12}{DC}=\dfrac{10+6}{6} \\
 & \dfrac{12}{DC}=\dfrac{16}{6} \\
\end{align}\]
By simplifying, we get:
\[DC=\dfrac{9}{2}\]
DC = 4.5 cm
For finding BD,
We know:
BD + DC = BC
By substituting, we get:
BD = 12 cm - 4.5 cm = 7.5 cm
Therefore the length of side BD and DC are 7.5 cm and 4.5 cm respectively.

Note: Apply the angle bisector theorem carefully. Observe that the bisector is from A or B. You should understand both cases. That’s why I wrote proof of bisector from B. Whereas the question asks us for a bisector from A.