Question

In a triangle ABC, AD is a median and E is midpoint of median AD. A line through B and E meets AC at point F. Is AC = 3AF? If True, then enter 1 else if False enter 0.

Answer 1

Hint: To solve this problem, we should know the basics of properties of a triangle. In this case, we will use the mid-point theorem to solve this question. According to this theorem, if we draw a line parallel to the base of the triangle from the midpoint of a side, then, it bisects the other side.

Complete step-by-step answer:
Now, before solving this question, we will make a simple construction. We will draw a line parallel to EF from point D (this is the line segment DG). Now, we make use of the mid-point theorem on two triangles. For reference, we will check the figure below.

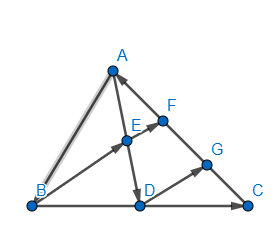
Now, we first refer to the triangle ADG, we have,
EF || DG (by construction)
Also, E is the midpoint of AD. Thus, by mid-point theorem which states that, if we draw a line parallel to the base of the triangle from the midpoint of a side, then, it bisects the other side, we have AF = FG. --(1)
Also, from triangle BCF, we have,
FG=GC -- (2)
Since, D is the midpoint of BC (AD is the median to BC). Also, DG || EF || BF (EF is part of the line BF).
From (1) and (2), we have,
AF=FG=GC
Since, AC = AF+FG+GC, we have,
AC = 3AF
Since, this is in fact true, we enter 1.

Note: While solving problems related to geometry of triangle, especially where we have to prove whether a point trisects a side or not, we should think about the usage of mid-point theorem since if one thinks about the usage of mid-point theorem, the use of construction in the geometry (in this problem, we had to construct an additional line segment DG) comes naturally.