Question

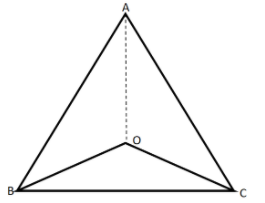
In a triangle $ABC$, $AB = AC$ and the bisector of angles $B$ and $C$ intersect at $O$. Prove that $BO = CO$ and $AO$ is the bisector of angle .
$\angle BAC$

Answer 1

Hint: Here we need to prove the given relation using the different properties of triangles. Here we have been given the two sides of a triangle are of equal length then the angles opposite to both the sides are also equal. Then using this property we will make two required triangles congruent. From there, we will get all our required answers.

Complete step-by-step answer:
According to question;
In $\vartriangle ABC$,
\[AB = AC\] and also \[OB\] bisect \[\angle B\] and \[OC\] bisect \[\angle C\].
We know that if two sides of a triangle are of equal length then the angles opposite to both the sides are also equal.
As \[AB = AC\] in $\vartriangle ABC$, so using this property, we get
\[\angle B = \angle C\] ………….. \[\left( 1 \right)\]
As it given that \[OB\] bisect \[\angle B\] and \[OC\] bisect \[\angle C\].
So we get,
\[\angle ABO = \angle OBC = \dfrac{{\angle B}}{2}\] ………… \[\left( 2 \right)\]
\[\angle ACO = \angle OCB = \dfrac{{\angle C}}{2}\] …………. \[\left( 3 \right)\]
Comparing equation \[\left( 1 \right)\], equation \[\left( 2 \right)\] and equation \[\left( 3 \right)\], we get
\[\dfrac{{\angle B}}{2} = \dfrac{{\angle C}}{2}\]
So we can write it as
\[ \Rightarrow \angle OBC = \angle OCB\] …………. \[\left( 4 \right)\]
And also we get
\[ \Rightarrow \angle ABO = \angle ACO\] …………… \[\left( 5 \right)\]
Now, we will consider $\vartriangle OBC$.
In $\vartriangle OBC$, we know from equation \[\left( 4 \right)\] that \[\angle OBC = \angle OCB\].
We know that if two sides of a triangle are of equal length then the angles opposite to both the sides are also equal.
Using this property here, we get
\[OB = OC\] ……… \[\left( 6 \right)\]
So we have proved that \[BO = CO\].
Now, we will consider $\vartriangle ABO$ and $\vartriangle ACO$ and we will make these two triangles congruent.
In $\vartriangle ABO$ and $\vartriangle ACO$, we have
\[\angle ABO = \angle ACO\] {From equation
\[\left( 5 \right)\]}
\[OB = OC\] {From equation \[\left( 6 \right)\]}
 \[AO = AO\] {As these are the common sides of both the triangles}
Therefore, we can say that $\vartriangle ABO$ and $\vartriangle ACO$ are congruent to each other i.e. $\vartriangle ABO \cong \vartriangle ACO$ by the SAS rule of congruence.
Therefore,
\[\angle BAO = \angle CAO\]
As these are the corresponding part of these congruent triangles, so we can say that \[AO\] is the bisector of angle \[\angle BAC\] .
Hence, we have proved both the relation.

Note: To solve this problem, we need to know the basic properties of the triangles. We need to remember that if two sides of a triangle are of equal length then the angles opposite to both the sides are also equal. Also the sum of all of the angles of a triangle is equal to \[180^\circ \].