Question

In a triangle ABC , AB = AC and $ \angle A = {36^o} $ . If the internal bisector of $ \angle C $ meets AB at point D, then:
AD = BC
AD = AC
AD = AB
AB = AC = BC

Answer 1

Hint: In order to solve this question we will first use the property of an isosceles triangle to find the angles which are unknown to us then as stated in question the line AD bisects the $ \angle C $ so the half angle be calculated. Now the half angle is known to us as well as the angle $ \angle B $ is calculated so we can find out the angle at which the D is touching AB on triangle BCD.

Complete step by step solution:
For solving this question as it is given in question that $ \angle A = {36^o} $ and AB = AC so according to the property of an isosceles triangle the two angles will be equal so we will let it as:
 $ \angle B = \angle C = {x^o} $

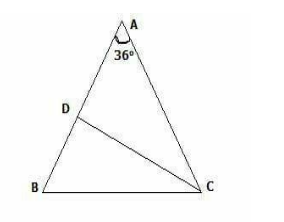
Now according to the property that the sum of all the angles of triangle is equal to $ {180^o} $
Now using this property we can write all the terms as:
 $ \angle A + \angle B + \angle C = {180^o} $
As we already know that two angles are equal and the value of one angle is already known so we will write it as:
 $ {36^o} + {x^o} + {x^o} = {180^o} $
Now on further this we will get:
 $ 2{x^o} = {144^o} $
On further solving we will get the value of:
 $ {x^o} = {72^o} $
So the values of angle B and C will be $ {72^o} $
The value of angle bisector of $ \angle C $ will be $ {36^o} $
Now as it is given in question that the line AD bisects the angle C and meets AB at D so we will bisects the angle C and find the value of $ \angle BCD $ so now in $ \Delta BCD $ :
So according to property of triangle:
 $ \angle BCD + \angle B + \angle BDC = {180^o} $
Now putting all the known values and find the unknown:
 $ {36^o} + {72^o} + \angle BDC = {180^o} $
Now substituting all the values to other side and finding the value of $ \angle BDC $ we will get:
 $ \angle BDC = {72^o} $
So we observed that the values of angle $ \angle BDC = {72^o} $ and $ \angle B = {72^o} $ as these two are equal so it means it is an isosceles triangle so according to its property we can say that:
AD = BC

So, the correct answer is “Option A”.

Note: While solving these types of problems we have to keep in mind that we are going in correct way to solve this question because if we directly go to find which two lines are equal we will not able to find it without finding the angle C so first to solve that and then we so of finding the rest.